
statistika
.docxВведение
Статистическое наблюдение, проведенное на основе официального учета или путем специально организованного изучения, дает огромное количество сведений, отраженных в статистических карточках, журналах учета и других первичных документах или в анкетах опроса граждан, изучения уголовных, административных, гражданских дел и других материалах. Получаемые сведения, как бы тщательно и научно обоснованно они ни собирались, представляют собой разрозненные "горы данных" о единицах изучаемой совокупности.
Для того чтобы выявить характерные черты этой совокупности и обнаружить связи между ее элементами, их закономерности, все собранные сведения (содержащиеся в документах первичного учета) необходимо систематизировать, подсчитать данные, расчленить по группам, соединить в целое, свести воедино, суммировать и подытожить результаты подсчетов, что достигается на втором этапе всякой законченной статистической работы -- в статистической сводке.
Статистическая сводка -- второй этап статистического исследования -- представляет собой проверку, систематизацию, научную обработку материалов статистического наблюдения. подытоживание отдельных единиц и сведения их в массы или совокупности в целях получения обобщенной характеристики изучаемого явления по ряду существенных для него признаков.
Группировка - это процесс образования групп единиц совокупности однородных в каком-либо отношении, а также имеющих одинаковые или близкие значения группировочного признака.
Чтобы решить ряд конкретных задач, выявить особенности в развитии явлений, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.
Задание №1 и 3
Для анализа использования материальных оборотных фондов предприятий одной из отраслей экономики произведена 5%-ная механическая выборка, результаты которой представлены в таблице:
Табл.1.
|
№ п/п |
Среднегодовая стоимость материальных оборотных фондов, млн.руб. |
Выпуск продукции, млн.руб. |
|
1 |
24,7 |
39 |
|
2 |
19,8 |
35 |
|
3 |
18,3 |
34 |
|
4 |
28,0 |
61 |
|
5 |
24,9 |
50 |
|
6 |
19,0 |
38 |
|
7 |
15,0 |
30 |
|
8 |
27,0 |
51 |
|
9 |
22,8 |
46 |
|
10 |
20,7 |
38 |
|
11 |
13,0 |
35 |
|
12 |
12,0 |
21 |
|
13 |
23,5 |
27 |
|
14 |
17,0 |
41 |
|
15 |
17,0 |
30 |
|
16 |
21,3 |
47 |
|
17 |
21,7 |
42 |
|
18 |
26,0 |
34 |
|
19 |
27,0 |
57 |
|
20 |
30,0 |
46 |
|
21 |
23,7 |
48 |
|
22 |
19,9 |
45 |
|
23 |
22,9 |
43 |
|
24 |
29,0 |
48 |
|
25 |
29,0 |
60 |
|
26 |
18,0 |
35 |
|
27 |
23,8 |
40 |
|
28 |
10,0 |
24 |
|
29 |
14,0 |
36 |
|
30 |
11,0 |
19 |
Решение:
1) Для анализа использования материальных оборотных фондов предприятий по размеру среднегодовой стоимости материальных оборотных фондов, пользуясь данными табл.1 построим интервальный вариационный ряд ряд распределения, характеризующий число предприятий и долю предприятий каждой группы.
Сначала определяем длину интервала по формуле:
h = (Xmax - Xmin) / n,
где Xmax и Xmin – максимальное и минимальное значение признака;
n – число групп, на которое разбивается совокупность.
В данной группе предприятий по среднегодовой стоимости материальных оборотных фондов видим, что
Xmax = 30,0;
Xmin = 10,0;
n=4 – группы предприятий.
h = (30,0– 10,0) / 4 = 5 (млн. руб.)
Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получим следующие группы предприятий по размеру среднегодовой стоимости материальных оборотных фондов. (табл.2.)
Распределение предприятий по размеру среднегодовой стоимости материальных оборотных фондов. Табл.2.
|
№ группы |
Группы организаций по среднегодовой стоимости материальных оборотных фондов, млн. руб. |
Число предприятий |
||
|
В абсолют- ном выражении |
В относи-тельных единицах,% |
Кумуля-тивная частота |
||
|
1 |
10-15 |
6 |
20 |
6 |
|
2 |
15-20 |
7 |
23,3 |
13 |
|
3 |
20-25 |
10 |
33,4 |
23 |
|
4 |
25-30 |
7 |
23,3 |
30 |
|
Итого: |
30 |
100 |
-- |
|
Данные группировки показывают, что 43,3% предприятий использовали среднегодовую стоимость материальных оборотных фондов на сумму 20 млн. руб. и выше, и 56,7% предприятий – на сумму свыше 20 млн. руб.
2). Для расчёта средней арифметической, среднего квадратического отклонения, коэффициента вариации применяем формулы во взвешенной форме, так как данные сгруппированы и представлены в виде интервального ряда.
Для расчета указанных величин нам понадобятся некоторые промежуточные данные, представленные в таблице 3:
Таблица 3
|
№ группы |
Группы предприятий по среднегодовой стоимости материальных оборотных фондов, млн.руб. |
Число предприятий (f) |
Середина интервала (х) |
х* f |
х-х |
(х-х)2* f |
|
1 |
10-15 |
6 |
12,5 |
75 |
-8 |
384 |
|
2 |
15-20 |
7 |
17,5 |
122,5 |
-3 |
63 |
|
3 |
20-25 |
10 |
22,5 |
225 |
2 |
40 |
|
4 |
25-30 |
7 |
27,5 |
192,5 |
7 |
343 |
|
Итого: |
- |
30 |
- |
615 |
- |
830 |
Данные для расчёта средней арифметической, среднего квадратического отклонения, коэффициента вариации
а) Для расчёта средней арифметической взвешенной применяют следующую формулу:
х = ∑ хf / ∑ f = 615/30 = 20,5 (млн. руб.)
где х – значение признака;
f – частота повторения признака;
∑хf – сумма произведений величины признаков на их частоты;
∑f – общая численность единиц совокупности.
б) Взвешенная дисперсия для вариационного ряда
σ2 = ∑(х-х)2 f / ∑ f = 830 / 30 = 27,7 (млн. руб.)
в) Среднее квадратическое отклонение для вариационного ряда вычисляется по формуле:


σ = ∑(х-х)2 f / ∑ fi = 27,7 = 5,26 (млн. руб.)
г) Тогда коэффициент вариации будет равен:
V = (σ /х)*100 = (5,26 / 20,5)100 = 25,66 %
т.к. V=25,66%<33% можно сделать вывод, что совокупность является количественно однородной по данному признаку.
Таблица 4.
Результаты расчёта средней арифметической, среднего квадратического отклонения, коэффициента вариации
|
№ п/п |
Показатель |
Значение |
|
1 |
Средняя арифметическая, млн. руб. |
20,5 |
|
2 |
Дисперсия, млн. руб. |
27,7 |
|
3 |
Среднее квадратическое отклонение, млн. руб. |
5,26 |
|
4 |
Коэффициент вариации, % |
25,66 |
Теперь вычислим среднюю арифметическую по данным таблицы 1.1, расчёт будем производить по формуле для среднеарифметической простой:
х = ∑ х / n = 630 / 30 = 21 (млн. руб.)
где х – значение вариант (индивидуальное значение признака у отдельных единиц совокупности);
n – число единиц совокупности.
Полученный результат отличен от приведённого выше, так как в данном случае расчет проводился для несгруппированных значений признака, представленных в виде дискретного ряда.
3). Мода (Мо) – представляет собой значение изучаемого признака, повторяющегося с наибольшей частотой.
Первоначально по наибольшей частоте определим модальный интервал. Наибольшее число предприятий – 10 – имеет среднегодовую стоимость материальных оборотных фондов в интервале 20-25 млн. руб., который и является модальным.
Мода среднегодовой стоимости материальных оборотных фондов:
f2 – f1 10– 7
Mо = x0 + I ——————— = 20 + 5 ————— = 22.5 (млн. руб.)
( f2 – f1 ) + (f2 - f3 ) (10 – 7) + (10 - 7)
где х0-нижняя граница модального интервала;
i-величина модального интервала;
f2-частота модального интервала;
f1-частота интервала, предшествующего модальному;
f3-частота интервала, следующего за модальным.
Значит, наиболее часто встречаемая среднегодовая стоимость материальных оборотных фондов 22,5 млн. руб.
Медиана (Ме) называется вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части.
Прежде всего найдем медианный интервал. Таким интервалом очевидно будет интервал среднегодовой стоимости материальных оборотных фондов предприятий (20-25 млн. руб.), поскольку его кумулятивная частота равна 23(6+7_10), что превышает половину суммы всех частот (30/2=15). Нижняя граница интервала 20 млн. руб., его частота 10;частота накопленная до него, равна 13.
Медиана среднегодовой стоимости материальных оборотных фондов:
(∑f) /2 – Sme -1 30 : 2 -13
Me = xме + iме —————— = 20 + 5 ————— = 21(млн. руб.)
fMe 10
где хме-нижняя граница медианного интервала;
Iме-величина медианного интервала;
∑f-сумма частот ряда;
SMe-1 –сумма накопленных частот ряда, предшествующих медианному.
Полученный результат говорит о том, что из 30 предприятий 50% имеют среднегодовую стоимость материальных оборотных фондов более 21 млн. руб., а 50% предприятий менее 21 млн. руб.
4). Согласно данным таблицы 3 построим графики полученного ряда распределения.




Рис. 1: Гистограмма распределения предприятий по среднегодовой стоимости материальных оборотных фондов

Рис. 2: Кумулята распределения предприятий по среднегодовой стоимости материальных оборотных фондов
5). а). Ошибка выборки
средней величины продукции и границы
 вычисляется как:
вычисляется как:
 ,
где:
,
где:
 - дисперсия по
признаку среднесписочная численность
работников,
- дисперсия по
признаку среднесписочная численность
работников,
 - объем выборочной
совокупности,
- объем выборочной
совокупности,
 -
объем генеральной совокупности.
-
объем генеральной совокупности.
Так как по условиям
выборка 5%-ная, то
 =
= /20*100=30/5*100
/20*100=30/5*100 60.
60.
 (млн. руб.)
(млн. руб.)
Это означает, что при выборке возможна ошибка 4,92 млн. руб.
Границы, в которых
будет находиться средняя величина
среднегодовой стоимости материальных
оборотных фондов в генеральной
совокупности, определяется как
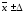 .
.
 ,
,
где t – нормированное отклонение и при вероятности 0,954, t=2.
 (млн. руб.)
(млн. руб.)
Границы, в которых
будет находиться средняя величина
среднегодовой стоимости материальных
оборотных фондов в генеральной
совокупности
 млн. руб., то есть средняя величина
среднегодовой стоимости материальных
оборотных фондов в генеральной
совокупности будет находиться в
промежутке от 10,66 до 30,34 млн. руб.
млн. руб., то есть средняя величина
среднегодовой стоимости материальных
оборотных фондов в генеральной
совокупности будет находиться в
промежутке от 10,66 до 30,34 млн. руб.
б). Ошибка выборки доли предприятий с среднегодовой стоимостью материальных оборотных фондов от 15 до 25 млн. руб.:
Количество предприятий с среднегодовой стоимостью материальных оборотных фондов от 15 до 25 млн. руб. равно 17.
Доля
 определяется как:
определяется как:
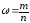 ,
,
где: m – количество единиц, обладающих признаком,
n – объем совокупности.
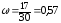
Дисперсия доли
 определяется как:
определяется как:
 .
.

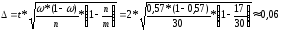
Генеральная доля будет находиться в пределах от 0,51 до 0,63, то есть от 51% до 63% от генеральной совокупности.
Вывод:
Таким образом, по результатам задания №1 и №3 можно сделать такой вывод: размер среднегодовой стоимости материальных оборотных фондов отличается от среднего размера среднегодовой стоимости материальных оборотных фондов в среднем на 5,26 млн. руб., что составляет 25,7%. Так как значение коэффициента вариации не превышает 33%, то изучаемую совокупность предприятий по среднегодовой стоимости материальных оборотных фондов можно считать однородной, а среднюю – типичной.
Задание №2
Решение:
Для изучения связи между явлениями и их признаками строят корреляционную таблицу и аналитическую группировку.
Сначала установим связь между указанными признаками методом аналитической группировки. В качестве факторного признака будет выступать среднегодовая стоимость материальных оборотных фондов, а в качестве результативного – выпуск продукции. Строим рабочую таблицу.
Результаты группировки отражены в таблице 5.
Таблица 5.
Зависимость выпуска продукции от среднегодовой стоимости материальных оборотных фондов
|
№ группы |
Группировка предприятий по среднегодовой стоимости материальных оборотных фондов, млн.руб. |
№ предприятия |
Среднегодовая стоимость материальных оборотных фондов, млн. руб. |
Выпуск продукции млн.руб.
|
|
I |
10-15 |
7 |
15,0 |
30 |
|
11 |
13,0 |
35 |
||
|
12 |
12,0 |
21 |
||
|
28 |
10,0 |
24 |
||
|
29 |
14,0 |
36 |
||
|
30 |
11,0 |
19 |
||
|
Итого: |
6 |
75 |
165 |
|
|
II |
15-20 |
2 |
19,8 |
35 |
|
3 |
18,3 |
34 |
||
|
6 |
19,0 |
38 |
||
|
14 |
17,0 |
41 |
||
|
15 |
17,0 |
30 |
||
|
22 |
19,9 |
45 |
||
|
26 |
18,0 |
35 |
||
|
Итого: |
7 |
129 |
258 |
|
|
III |
20-25 |
1 |
24,7 |
39 |
|
5 |
24,9 |
50 |
||
|
9 |
22,8 |
46 |
||
|
10 |
20,7 |
38 |
||
|
13 |
23,5 |
27 |
||
|
16 |
21,3 |
47 |
||
|
17 |
21,7 |
42 |
||
|
21 |
23,7 |
48 |
||
|
23 |
22,9 |
43 |
||
|
27 |
23,8 |
40 |
||
|
Итого: |
10 |
230 |
420 |
|
|
IV |
25-30 |
4 |
28,0 |
61 |
|
8 |
27,0 |
51 |
||
|
18 |
26,0 |
34 |
||
|
19 |
27,0 |
57 |
||
|
20 |
30,0 |
46 |
||
|
24 |
29,0 |
48 |
||
|
25 |
29,0 |
60 |
||
|
Итого: |
7 |
196 |
357 |
|
Для установления наличия и характера связи между среднегодовой стоимостью материальных оборотных фондов и выпуском продукции по данным рабочей таблицы 6 строим итоговую аналитическую таблицу.
Таблица 6
Зависимость среднегодовой стоимости материальных оборотных фондов от выпуска продукции
|
Группировка предприятий по среднегодовой стоимости материальных оборотных фондов, млн. руб. |
Число пред-прия-тий |
Среднегодовая стоимость материальных оборотных фондов, млн. руб. |
Выпуск продукции, млн. руб. |
||
|
Всего |
В среднем на одно пр-тие |
Всего |
В среднем на одно пр-тие |
||
|
10-15 |
6 |
75 |
12,5 |
165 |
27,5 |
|
15-20 |
7 |
129 |
18,43 |
258 |
36,86 |
|
20-25 |
10 |
230 |
2,3 |
420 |
42 |
|
25-30 |
7 |
196 |
28 |
357 |
51 |
|
Итого: |
30 |
630 |
81,93 |
1200 |
157,36 |
По данным аналитической таблицы мы видим, что с ростом среднегодовой стоимости материальных оборотных фондов, выпуск продукции в среднем на одно предприятие возрастает. Значит, между исследуемыми признаками существует прямая корреляционная зависимость.
Материалоотдача характеризует стоимость продукции на один рубль материальных оборотных фондов.
Мо = В/Мз ,
Мо = 1200/630 =1,91 руб.
Материалоёмкость отражает величину материальных затрат приходящихся на 1 рубль выпущенной продукции.
Ме= Мз/В = 630/1200 = 0,53 руб.
2). Для того чтобы
определить тесноту взаимосвязи между
факторным и результативным признаком
необходимо вычислить эмпирическое
корреляционное отношение -
 .
.
Корреляционное отношение вычисляется как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии.
η=√δ2/σ2
Для этого необходимо вычислить:
-
Среднюю из внутригрупповых дисперсий;
-
Межгрупповую дисперсию;
-
Общую дисперсию.
Рассчитаем среднюю из внутригрупповых дисперсий по формуле:

