ФГБОУ ВПО Уфимский государственный авиационный технический университет

Кафедра Информатики

100	1	2	3	4	5	6	7	8	9	10	11	12
90
80
70
60
50
40
30
20
10

Выполнение индивидуального задания

в MS Word

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к лабораторной работе по

информатике

1308.501106.000ПЗ

(обозначение документа)

Группа			Фамилия, И., О.		Подпись		Дата		Оценка
	ФЭБ-110
Студент				Мустафина Л.И.
Консультант				Янгирова А.Ф.
Принял

Уфа 2013 г.

Содержание

Введение 3

1. Численное решение уравнений 4

1.1 Метод хорд (пропорциональных частей) 4

1.2 Алгоритм метода хорд 5

Заключение 7

Список литературы 8

Введение

Для того чтобы уметь решать конкретные задачи на компьютере, недостаточно уметь правильно писать операторы на каком-либо языке программирования. Необходимо, прежде всего, знать алгоритмы и методы их решения.

В научных исследованиях и инженерном проектировании часто приходится решать уравнения вида

Задачи этого типа могут возникать сами по себе или же составлять часть более сложных исследований.

Пример. Сила тока в цепи изменяется по закону

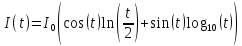
Определить точки смены знака тока. Задача сводится к решению уравнения

Возможности аналитического решения уравнений являются достаточно ограниченными. Поэтому для нахождения корней уравнений привлекаются методы приближенных (численных) вычислений с заданной степенью точности [1]

1. Численное решение уравнений

Для вычисления корня уравнения существует множество приближенных методов. Все они вычисляют значение корня уравнения с заданной степенью точности

1.1 Метод хорд (пропорциональных частей)

При изложении методов численного решения уравнений будем считать, что нам уже известен отрезок [a,b] , внутри которого существует один и только один корень.

Идея метода хорд состоит в том, что, кривую y=f(x) на достаточно малом участке можно заменить хордой, и в качестве начального приближенного значения корня принять точку пересечения хорды, проходящей через точки (a, f(a)) и (b, f(b)) с осью абсцисс. Полученное значение можно снова использовать для дальнейшего уточнения корня по способу хорд, рассматривая тот интервал, в котором лежит истинный корень, т.е. тот, на концах которого функция имеет разные знаки. Таким образом, получается следующее приближение корня.

Рисунок 1. 0 .1 представляет графическую интерпретацию метода хорд.

Рисунок 1.0.1–Графическая интерпретация метода хорд

Уравнение прямой, проходящей через точки с координатами (a, f(a)) и (b, f(b)) , имеет вид

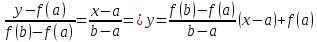. ( 1.0.0)

Прямая, заданная уравнением (1.1), пересекает ось Ox при условии y = 0. Точку пересечения хорды с осью Ox можно вычислить по формуле

откуда

c=a-. ( 1.0)

1.2 Алгоритм метода хорд

Метод хорд реализуется в виде следующего алгоритма:

1. По формуле (1.2) найти точку с.

2. Выбирается отрезок, в котором находится корень: если , то корень лежит на интервале [a,b] если нет, то корень лежит на интервале [c,d]. В первом случае b=c, во втором a=c.

3. Если абсолютное значение f(c) не превышает некоторое достаточно малое число , то найден корень с точностью , иначе возврат к п. 1.

Рисунок 1.2 представляет блок-схему алгоритма метода хорд.

Рисунок 1.2– Блок-схема алгоритма метода хорд

Ниже (таблица 1.1) приведены результаты пошагового вычисления корня уравнения на отрезке методом хорд¹.

Таблица 1.1

№ шага	x
1.	1,0981	0,0422
2.	1,1413	0,0179
3.	1,1592	0,0073

Заключение

Метод хорд удобно применять для грубого нахождения корня уравнения, метод прост и надежен. Этот метод позволяет достаточно быстро (за меньшее количество шагов, чем в методе половинного деления) вычислить значение корня уравнения с заданной точностью.

Список литературы

1. .Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука, 1972. 366 с.

2. Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах MathCad 12, MatLab 7, Maple 9. М.: НТ Пресс, 2006. 496 с.

1 Вычисления проводились с точностью 0,01