73. Геометрические меры информации. Каким образом они представлены в индикаторах сои?
Количество меры информации при использовании геометрической меры определяется путём измерения длины линии, площади или объема геометрической модели в количестве дискретных единиц (квантах).
n
– Мера информации в геометрической
структуре.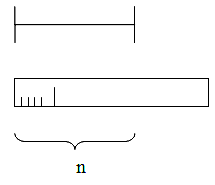
Можно определить потенциальные, т.е. максимально возможное количество информации в заданных структурных габаритах, которые называют информационной ёмкостью исследуемой части информационной системы, она может быть представлена числом, показывающим количество квантов в полном массиве информации.
Если дискретные отсчеты осуществляются по осям X,T, N через интервалы ΔX, ΔT, ΔN, то непрерывные коэффициенты распадаются на элементы кванты количество которых:
;
;
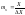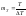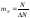
а количество информации определяемых геометрическим методом:
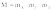
в индикаторах СОИ геометрические меры информации представлены в виде дискретных значений шкальных индикаторов и ЖК индикаторов измеряемой величины (давления, высоты, и т.д.)
74. Количество информации. Аддитивные меры Хартли.
Процесс получения информации математически характеризуется изменением распределения вероятности множества различных сообщений. В математическом (операционном) аспекте, это изменение распределения вероятности и есть «информация». Соответственно ее количественная мера (количество информации) и устанавливается как некоторый числовой показатель (функционал), характеризующий отличие апостериорных распределений плотности вероятности различных сообщений от априорного. Такая точка зрения впервые четко была сформулирована К. Шенноном и им же весьма удачно выбрана количественная мера, на основе которой доказаны важнейшие теоремы, определяющие предельно достижимые значения некоторых показателей сообщений и информационных систем.
Количество информации, содержащейся в сообщении, по Шеннону определяется в виде I = Hapr — Haps, где Нapr и Haps — числовые показатели (функционалы), характеризующие априорные и апостериорные распределения вероятностей различных сообщений.
Здесь Нapr и Нара соответственно априорная и апостериорная энтропия системы. Априорная энтропия полностью характеризуется распределением вероятностей состояний системы с учетом статистических связей. Апостериорная энтропия характеризует ту неопределенность системы, которая остается после приема сообщений. Если сообщение однозначно определяет состояние системы, то Нapr=0, в противном случае Haps>0.
Глубина h числа– количество элементов, знаков,
содержащихся в принятом алфавите.
Глубина числа соответствует основанию
системы счисления и кодирования.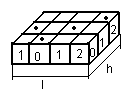
В каждый данный момент реализуется только один знак из hвозможных.
Длина lчисла – количество повторений алфавита, необходимых и достаточных для представления чисел нужной величины. Длина числа соответствует разрядности системы счисления и кодирования.
При глубине hи длинеlколичество чисел выразится:Q=h l , т.е. емкость зависит экспоненциально от длины числаl.
Пример:
h=1 унарная система
счисления.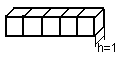
h=2двоичная система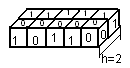
h=3…10
-------------------------
В следствии показательного закона зависимости Qотl, числоQне является удобной мерой для оценки информационной емкости, поэтому Хартли ввел аддитивную двоичную логарифмическую меру, позволяющую вычислять количество информации в двоичных единицах – битах. Для этого берется не само числоQ, а его двоичный логарифм.
I = log2Q = log2h l = llog2h,
где I– количество информации по Хартли.
Если длина числа l = 1 и принята двоичная система счисления, то
I=log221=1
(бит)
Это единица информации в принятой системе оценки. Она соответствует одному элементарному событию, кот. Может произойти (1) или нет (0). Аддитивная мера удобна тем, что она обеспечивает возможность сложения, а также пропорциональность количества информации длине числа l.