49. Частотно-импульсная модуляция. Спектр и полоса частот

Модулированные колебания имеют сложный спектральный состав, причем каждому виду модуляции соответствует свой спектр амплитуд и спектр фаз. Для анализа процессов демодуляции модулированных колебаний необходимо знать их спектры.

Модуляции может подвергаться амплитуда ; частотаили фаза, соответственно имеем амплитудную (АМ), частотную (ЧМ) или фазовую (ФМ) модуляции.

Преобразователи, в которых несущие колебания модулируются, называются модуляторами. При частотной модуляции (ЧМ) в соответствии с модулирующей величиной изменяется частота несущего сигналагде- наибольшее изменение частоты модулирующего сигнала или девиация частоты.

По определению фаза

Откуда видно, что частотная модуляция сопровождается фазовой.Частотно – модулированный сигнал выразится,где- глубина модуляции.

Рассмотрим спектральный состав ЧМ – колебаний.

- девиация- индекс частотной модуляции

При малых

ЧИМ

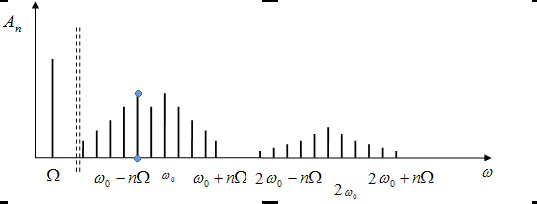
51. Амплитудно-импульсная модуляция. Спектр и полоса частот

Непрерывная физическая величина, например, напряжение или ток, изменяющаяся по гармоническому закону, определяется как

где параметры гармонического колебания. У немодулированного колебания все 3 параметра постоянны. Процесс управления (изменения) любым из параметров посредством измеряемой (передаваемой, преобразуемой) величины называется модуляцией, а саму величину называют модулирующим сигналом.

Модуляции может подвергаться амплитуда ; частотаили фаза, соответственно имеем амплитудную (АМ), частотную (ЧМ) или фазовую (ФМ) модуляции.Преобразователи, в которых несущие колебания модулируются, называются модуляторами. Пусть модулирующий сигнал задан функцией. Тогда при амплитудной модуляции (АМ), т.е. при воздействии сигналом на параметр, получим

где - глубина модуляции,;- девиация амплитуды или наибольшее изменение амплитуды модулируемого сигнала.

- закон изменения модулирующего сигнала, причем .

Если амплитудная модуляция осуществляется таким образом, что в отсутствие модулирующего сигнала амплитуда несущего колебания равна нулю, то получим модулированный сигнал

Такой вид модуляции называется балансной (БАМ).

Известно, что периодическая функция может быть представлена рядом Фурье

,где - период функции;

Т.е периодическую функцию определяет совокупность амплитуд, которую называют спектром амплитуд, и совокупность начальных фаз, которую называют спектром фаз.

Модулированные колебания имеют сложный спектральный состав, причем каждому виду модуляции соответствует свой спектр амплитуд и спектр фаз. Для анализа процессов демодуляции модулированных колебаний необходимо знать их спектры.

Спектры при разных видах модуляции целесообразно сопоставить при одинаковом входном воздействии. Обычно это гармонический сигнал низкой частоты

Где - амплитуда модулирующего сигнала,

- его частота.АМ колебание при .

где - глубина модуляции,

s - крутизна модуляционной характеристики.

Тогда

Видим три составляющие: несущую с частотойи две боковые с частотами(боковые или комбинационные). Отметим, что в спектре АМ колебания отсутствует составляющая с частотой модулирующего сигнала.

При БАМ модулированное колебание

т.е колебания с несущей частотой отсутствуют.