41. Частотная фильтрация.

43 . Базисные функции.

К системе базисных функций предъявляют следующие основные требования:

- для любого колебания (ряд должен сходиться);

- базисные функции должны иметь принятую аналитическую форму ;

-коэффициенты ряда должны вычислятся относительно просто.

Этим условиям удовлетворяют системы ортогональных функций.

Условия ортогональности функции имеет вид:

при i≠k, где i и k –натуральные числа

при i=k :

Пример:sinωt cosωt

sin2ωt cos2ωt

sin3ωt cos3ωt

sin4ωt cos4ωt

…. ….

- норма базисной функции.

Каждую базисную функцию можно пронормировать по ее норме. Тогда нормированная базисная функция будет иметь вид: , в этом случае новая система будет удовлетворять не только условно ортогональности, но и условию нормировки:

, где

- символ Кронекера для ортогональных ф-ций

Рассмотрим как определяются коэффициенты при разложении колебания по системе ортонормированной функциии

или (*) где-нормированная функция.

Умножим части уравнения на и проинтегрируем на интервалеt1-t2:

По условию ортонормированности следует, что в правой части полученного уравнения все интегралы при i≠k равны 0, а при i=k – равны 1. Следовательно:

Фурье показал, что полученные коэффициенты являются оптимальными для данного ряда (*). Принципиально число членов ряда → ∞, но для реальных колебаний всегда можно указать небольшое число членов этого ряда, при котором погрешность вполне допустима.

Для разложения можно использовать элементарные функции, а так же ряд специальных систем функций.,обладающих свойством ортогональности : тригонометрические функции кратных аргументов, полиномы Эрмита, Лемандра, Чебышева, функция Бесселя, Лагерра.

Для теоретического анализа целесообразно выбирать сисетму функций, обеспечивающую наиболее быструю сходимость ряда в ряде случаев решающим при выборе является простота физического осуществления, т.е. генерирования функции. Таким свойством обладает система тригонометрических функций кратных аргументов. В более широком смысле это соотношение называют рядом Фурье независимо от вида базисных ортогональных функций.

45. Демодуляция чм гармонических колебаний

42. Спектральная плотность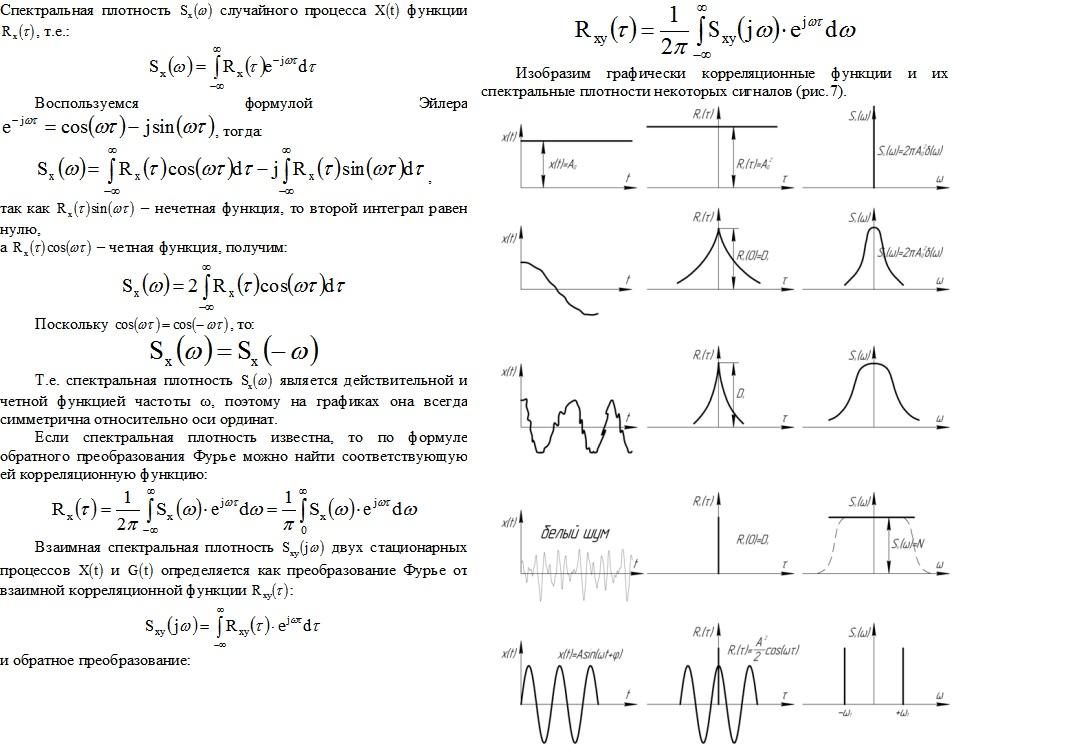

53. Квантование во времени. Теорема отсчетов.

47. Корреляционный метод фильтрации

46. Преобразование Фурье.

Переход от периодической последовательности импульсов S(t) к одиночному импульсу V(t) осуществляется следующим образом: будем безгранично увеличивать период следования последовательности импульсов t, сохраняя длительность tи и форму не изменой. При этом частота первой гармоники будет понижаться, стремясь в предел к бесконечно малой величине: 1/Т=f1→df при t→∞.

Соответственно расстояние между гармониками будет стремиться к dω

Следует иметь в виду, что для различной формы импульсов огибающая будет различна.

Практически удобней применять ряд Фурье записанный в комплексной форме:

Для импульсов: (T→∞, A_K→0)

Так как величина перед интегралом при Т→∞ бесконечно малое, следовательно и амплитуды составляющих так же будут бесконечно малые. По-этому спектр одиночного импульса представляется как бесконечное множество гармоничных состаляющих всех частот от 0 до ∞ с бесконечно малыми амплитудами всех этих составляющих.

Пользоваться бесконечно малыми величинами неудобно, поэтому для наглядности и удобства вместо амплитуд Ак изображают величину их отношений к частоте первой гармоники (1/Т=f1).

эту величину называют спектральной функцией или спектральной характеристикой, соответствующей импульсу U(t). Она является комплексной функцией частоты определенной при положительных и отрицательных значениях частоты. Вид спектральной ф-ии зависит только от формы импульса U(t).

- прямое преобразование.

Для решения обратной задачи, т.е. вычисления характеристик импульса U(t) через его спектральную функцию применяют обратное преобразование Фурье:

- обратное преобразование.

На вход подаются :

Преобразование только для детерминированных сигналов

U P=U*i

I P=i²*R

R P=U²/R

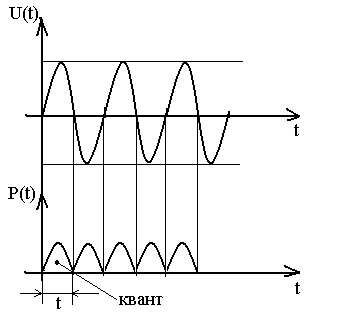Pk – амплитуда мощности.

Переход от амплитуд, характеризующих мощность энергии Ак(ω) к спектру мощности называют спектральной плотностью мощности Рк(ω)

Чем дальше, тем меньше кванты. На определенном уровне (Ω – 1 квант, 2 Ω–2 кванта… )

На постоянном токе – 1 квант. Можно считать, что нет кванта энергии, так как он долго тянется.