Аналитич геометрия в пространстве
.docxАНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
-
Поверхности и линии в пространстве
Определение 1.
Уравнением
поверхности (в фиксированной системе
координат) называется такое уравнение
с тремя переменными
,
которому удовлетворяют координаты
любой точки данной поверхности и только
они.
Здесь
– некоторая зависимость между
переменными
.
Пример 1.
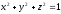– уравнение сферы (
).
Определение 2. Линию в пространстве можно рассматривать как пересечение двух поверхностей, поэтому она определяется двумя уравнениями:
.
Пример 2.
.
Линия, как пересечение
поверхностей, определяет окружность,
лежащую в плоскости
(
).
2. Уравнение плоскости по точке и нормальному вектору
Дано:
,
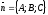– нормальный вектор,
.
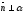Написать уравнение плоскости.
Выберем произвольную
точку
,
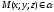тогда
,
,
т.е.
|
(1) |
|
– уравнение плоскости.
3. Общее уравнение плоскости
Из уравнения (1) с
помощью элементарных преобразований
получим:
или
|
(2) |
|
– общее уравнение плоскости.
Очевидно, что общее
уравнение плоскости является алгебраическим
уравнением первого порядка относительно
трех переменных
и определяет поверхность
первого порядка.
Проведем исследование (положение плоскости в частных случаях).
А)
,
.
Т.к. координаты
точки
- удовлетворяют данному уравнению,
плоскость проходит через начало
координат.
Б)
,
,
,
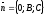значит
,
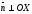следовательно
.
Аналогично, если
,
;
,
.
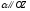В) При
,
.
Плоскость проходит через ось
.
Аналогично, при
– плоскость проходит через ось
;
при
– плоскость проходит через ось
.
Г)
,
.
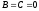Данное уравнение определяет плоскость,
параллельную
,
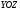т.к.
,
,
.
Аналогично,
,
;
,
.
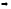
Д)
,
(
).
Аналогично,
,
(
);
,
(
).
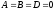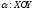4. Уравнение плоскости в отрезках
,
,
.
|
(3) |
|
.– уравнение плоскости в отрезках.
-
Уравнение плоскости по трем точкам
Пусть
.
Выберем произвольную
точку
.
Тогда
,
,
.
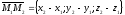Т.к. векторы лежат
в одной плоскости, они компланарны,
следовательно их смешанное произведение
равно нулю:
|
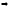
(4) |
|
.– уравнение плоскости по трем точкам.
-
Нормальное уравнение плоскости
Нормальное уравнение плоскости строится по аналогии с нормальным уравнением прямой и имеет вид:
. (5)
7. Взаимное расположение плоскостей в пространстве
Пусть
- нормальный вектор для плоскости
.
Утверждение 1.
Вектор
параллелен плоскости
,
заданный уравнением (14.2) тогда и только
тогда, когда
. (6)
Утверждение 2.
Плоскость
,
заданная уравнением
и плоскость
,
заданная уравнением
параллельны тогда
и только тогда, когда
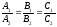. (7)
Доказательство.
Действительно,
,
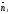если
и
коллинеарны, т.е.
,
,
,
т.е.
.
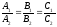Верно и обратное.
Утверждение 3.
Плоскости
и
совпадают тогда и только тогда, когда
. (8)
Утверждение 4.
Плоскости
и
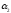пересекаются тогда и только тогда, когда
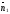и
неколлинеарны, причем угол между ними
равен углу между нормальными векторами.
Утверждение 5.
Пусть плоскости
и
пересекаются по прямой, тогда плоскость
проходит через эту прямую, причем ее
уравнение имеет вид:
,
где
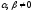одновременно. (14.9)
8. Уравнение прямой в пространстве
Поскольку пересекающиеся плоскости пересекаются по прямой, то
(10)
причем
(11)
Система уравнений (10) с условием (11) называется общим уравнением прямой в пространстве. Данная система линейных неоднородных уравнений совместна и имеет общее решение следующего вида:
|
(12) |
|
,
где
– частное решение (10),
– фундаментальная система решений
соответствующей системы линейных
однородных уравнений.
Геометрически (12) означает следующее:
Пусть точка
.
Любая точка
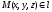получается прибавлением к радиус-вектору
точки
некоторого вектора, коллинеарного
- направляющего вектора прямой.
Уравнение (12) можно
переписать в виде
или
,
(13)
– векторно-параметрическое
уравнение прямой
или
(14)
– параметрические уравнения прямой в пространстве.
Исключая параметр
,
получим:
|
(15) |
|
– канонические уравнения прямой в пространстве.
Здесь равенства (15) следует воспринимать как пропорцию.
Пример 3. Пусть прямая задана каноническими уравнениями
(*). Тогда уравнения
(*) равносильны системе:
,
.
Если необходимо
написать уравнение прямой, проходящей
через две точки
и
,
то
– направляющий вектор, тогда
|
(16) |
|
– уравнение
,
проходящей через 2 точки.
Утверждение 6.
Если прямая
,
задана как пересечение двух плоскостей
системой (.10), то вектор
(17)
– является
направляющим вектором
,
т.е.
.
9. Взаимное расположение двух прямых в пространстве
Пусть
;
.
и
либо пересекаются, либо параллельны (в
частном случае совпадают), либо
скрещиваются.
.
В случае если
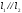или пересекаются, существует плоскость,
которой прямые принадлежат. Поэтому
выполняется условие:
. (18)
Утверждение 7.
Прямые
и
скрещиваются тогда и только тогда, когда
. (19)
-
Если прямые пересекаются, то может решаться задача нахождения угла между прямыми. В этом случае угол определяется углом между направляющими векторами.Если прямые параллельны, то возникает задача нахождения расстояния между ними:
Плоскость, содержащая
параллельные прямые, имеет вектор
нормали
,
,
тогда
Замечание: A)
,
т.е.
,
B)
,
т.е.
.
-
Если прямые скрещиваются, то расстояние между ними равно высоте параллелепипеда, построенного на векторах
,
т.е.
