
- •Сборник ответов к экзамену «Теория вычислительных процессов»
- •Раздел 1. Асинхронные процессы (ап)
- •Простой асинхронный процесс. Протокол простого ап.
- •Репозиция ап. Автономный асинхронный процесс.
- •Конвейерный принцип обработки информации.
- •Редукция асинхронного процесса. Свойства редукции.
- •Структурирование ситуаций ап.
- •Диаграмма переходов (дп). Конфликтная ситуация. Полумодулярная дп.
- •Редукция диаграммы переходов.
- •15. Основная идея теории комплектов, сравнение с теорией множеств. Свойства комплектов.
- •32. Помеченные сети Петри. Пример.
- •33. Префиксный язык сети Петри. Свободный терминальный язык сети Петри. Терминальный язык сети Петри. Пример.
- •34. Три вида помечающих функций для сетей Петри.
- •35. Классы языков сетей Петри. Пример.
- •36. Стандартная форма помеченных сетей Петри
- •40. Методы анализа сетей Петри: дерево достижимости. Пример.
- •41. Средства ограничения дерева достижимости до определенных (конечных) размеров.
- •42. Алгоритм построения дерева достижимости.
- •43. Лемма 1 для доказательства теоремы о конечности дерева достижимости сети Петри.
- •44. Лемма 2 для доказательства теоремы о конечности дерева достижимости сети Петри.
- •45. Лемма 3 для доказательства теоремы о конечности дерева достижимости сети Петри.
- •46. Терема о конечности дерева достижимости сети Петри.
32. Помеченные сети Петри. Пример.
Определение. Помеченная сеть Петри – это пара (C,Σ), где С=(Р, Т, I, О), Σ: Т→А – помечающая функция над некоторым алфавитом А.
На рисунке показан пример помеченной сети Петри (C, Σ) над алфавитом {a, b, c}:
Σ: Σ(t1)= a, Σ(t2)= c, Σ(t3)= b, Σ(t4)= c.

Рис. 40. Пример помеченной сети Петри
В зависимости от вида получают различные классы языков сетей Петри.
Если Σ – частичная функция, т.е. некоторым переходам не сопоставляется никакой символ из А, то эти непомеченные переходы называются λ-переходами и помечаются одним и тем же «пустым» символом λ.
Частичные функции удобны в тех случаях, когда при моделировании системы нужно ввести вспомогательные переходы, не связанные непосредственно с событиями системы, а используемые для некоторых специальных целей моделирования. С помощью λ-переходов также можно «маскировать» события, которые не должны рассматриваться в данной задаче моделирования.
33. Префиксный язык сети Петри. Свободный терминальный язык сети Петри. Терминальный язык сети Петри. Пример.
Пусть
τ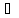 T*
- допустимая последовательность запусков
переходов сети Петри C,
(C,
Σ)
– помеченная сеть, Σ
(τ)
T*
- допустимая последовательность запусков
переходов сети Петри C,
(C,
Σ)
– помеченная сеть, Σ
(τ)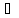 A*
- помечающая последовательность,
соответствующая τ.
A*
- помечающая последовательность,
соответствующая τ.
Определение.
Если L(C)
– свободный язык сети Петри C, то множество
{Σ
(τ)| τ L(C)}
называется префиксным языком помеченной
сети (C,
Σ).
L(C)}
называется префиксным языком помеченной
сети (C,
Σ).
Обратите внимание на тот факт, что если A=T, то свободный язык СП совпадает с ее префиксным языком.
Во многих случаях бывает удобно или необходимо рассматривать не свободный язык сети Петри, включающий все ее последовательности запусков переходов, а только его подмножество. Пусть μ0 – начальная маркировка СП, а μt – некоторая фиксированная терминальная маркировка.
Определение.
Множество L(C,μ0,μt)={τ T*|δ(μ0,τ)=μt}
называется свободным терминальным
языком сети Петри C.
T*|δ(μ0,τ)=μt}
называется свободным терминальным
языком сети Петри C.
Другими словами, свободный терминальный язык состоит из всех последовательностей переходов, ведущих от начальной маркировки μ0 к некоторой фиксированной терминальной маркировке μt. Такие последовательности образуют подмножество терминальных последовательностей СП.
Соответственно
множество {Σ(τ)|τ L(C,μ0,μt)}
образует терминальный язык помеченной
сети (C,Σ).
L(C,μ0,μt)}
образует терминальный язык помеченной
сети (C,Σ).
Например, пусть τ1, τ2 - допустимые последовательности запусков переходов некоторой сети Петри, ведущие из некоторой начальной маркировки в некоторую заключительную и других таких
последовательностей не существует: τ=t1t1; τ=t2t4t3t3t3.
Тогда префиксный язык: {t1, t1t1, t2t4t3t3t3, t2t4t3t3, t2t4t3, t2t4, t2}; терминальный язык: {t1t1, t2t4t3t3t3}.
34. Три вида помечающих функций для сетей Петри.
Вид
1.
Σ(tj)=tj
для
 tj
tj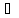 T
– свободная помечающая функция (ПФ).
T
– свободная помечающая функция (ПФ).
Вид
2.
Σ(tj)
определена для
 tj
tj T
пометки – символы из А. Это всюду
определенная помечающая функция. Сеть
без λ-переходов.
T
пометки – символы из А. Это всюду
определенная помечающая функция. Сеть
без λ-переходов.
Вид
3.
Σ(tj)
не
определена для некоторых переходов,
т.е. tj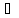 T
–
такой переход, tj
помечается
пустым символом λ
и объявляется λ-переходом.
Тогда это частично определенная
помечающая функция.
T
–
такой переход, tj
помечается
пустым символом λ
и объявляется λ-переходом.
Тогда это частично определенная
помечающая функция.
35. Классы языков сетей Петри. Пример.
Пусть N – класс всех сетей Петри. На основе введенных ранее понятий и видов помечающих функций (свободная ПФ, всюду определенная ПФ и частично определенная ПФ) можно образовать следующие классы языков сетей Петри.

В данном случае верхний индекс λ означает, что ПФ могут быть частично определенными, то есть сеть может содержать λ-переходы.
Верхний индекс f означает, что используются свободные ПФ.
Нижний индекс 0 означает, что рассматриваются терминальные языки.
Пример 31. Рассмотрим сеть Петри с различными вариантами помечающей функции, для каждой найдем префиксный и терминальный языки (Рис. 41).

Рис. 41. Помеченная сеть Петри для примера 31
Пусть μ0=(1000), μt=(0001).
Допустимые последовательности запусков:
1) t2t4;
2) (t1 ...t1) t2 (t3 ...t3) t4
n1 раз n2 раз
Варианты помечающей функции:
Свободная ПФ – Σ1(tj)=tj.
Префиксный
язык: L(C)={t2
,t2
t4
,t1n1
,t1n1
t2
,t1n1
t2
t3n3
,t1n1
t2
t3n3
t4:
n1 1,
n1
1,
n1 n3}=
n3}=
={t1n1
t2n2
t3n3
t4n4:
0≤n1,
0 n2
n2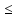 1,
0
1,
0 n3
n3 n2*n1,
0
n2*n1,
0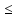 n4
n4 n2}.
n2}.
Терминальный
язык: L(C,
μ0,
μt)={t1n
t2
t3n
t4
,t2
t4:n N0}.
N0}.
2) Пусть Σ2 - всюду определенная помечающая функция, сеть не содержит λ-переходы (табл. 3).

Всюду определенная помечающая функция для примера 31
Префиксный
язык: L(C,
Σ2)
={ an1bn2:
n1 1,
0
1,
0 n2
n2 n1}.
n1}.
Терминальный
язык: L(C,
Σ2,
μ0,
μt)
={anbn:
n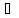 N}.
N}.
3) Пусть Σ3 - частично определенная помечающая функция, сеть содержит λ-переходы (табл. 4).

Частично определенная помечающая функция для примера 31
Префиксный
язык: L(C,
Σ3)
={an1bn2cn3:
0 n1
n1 1,
(n1=0→n2=0),
(n1=1→n2=1),
0
1,
(n1=0→n2=0),
(n1=1→n2=1),
0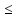 n3
n3 n1}.
n1}.
Терминальный язык: L(C, Σ3, μ0, μt) ={abnc: n≥0}.
