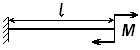Вопросы и задачи по курсу МСС, 2012

124. Что такое полярный момент инерции? В каких единицах он измеряется?

125. Из условия прочности подобрать сечение балки из стали 3 ( = 120 МПа), если М = 15 кНм, l = 5 м.

126. При растяжении силой F = 40 кН плоского образца с поперечным сечением 40х10 мм и длиной 250 мм его удлинение оказалось равным 150 мкм, а уменьшение большего поперечного размера составило 6 мкм. Определите модуль упругости и коэффициент Пуассона материала.

127. Как изменится угол закручивания вала, если крутящий момент увеличить в 4 раза, а диаметр уменьшить в 2 раза?

128. Как изменится максимальное напряжение в поперечном сечении круглого вала при кручении, если диаметр вала уменьшить в 2 раза?

129. Образец с диаметром 40 мм разрушился при крутящем моменте 230 Нм. Определите разрушающее напряжение.

130. Из условия прочности подобрать сечение балки из стали 3 ( = 90 МПа), если М = 10 кНм, l₁ = 2 м, l₂ = 2 м.

131. Из расчета на прочность определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала – сталь, допускаемое напряжение при кручении 30 МПа.

132. Из условия прочности подобрать сечение балки из стали 3 ( = 140 МПа), если Р = 20 кН, l₁ = 1 м, l₂ = 1 м.

133. Рассчитать на прочность балку из стали3 ( = 100 МПа), если М = 15 кНм, l₁=1м, l₂ = 3 м.

134. Определите осевые моменты инерции квадратного сечения со сторонами а с центральным круглым отверстием диаметра d = 0,5а относительно осей симметрии.

135. При растяжении силой F = 40 кН плоского образца с поперечным сечением 1040 мм и длиной 250 мм его удлинение оказалось равным 150 мкм, а уменьшение большего поперечного размера составило 6 мкм. Определите коэффициент Пуассона материала.

136. Во сколько раз изменится относительное удлинение круглого стержня, если его диаметр уменьшить в 2 раза?

137. Стальной круглый вал длиной 5 м защемлен одним концом и нагружен на другом скручивающим моментом, под действием которого точка, взятая на поверхности вала на свободном конце, перемещается по дуге длиной 5 мм. Чему равны наибольшие касательные напряжения в вале, если модуль сдвига материала G = 80 ГПа?

Новые (2012г.)

138. Определить прогиб точки приложения силы круглого стального бруса с диаметром 40 мм, если Р = 10 кН, l1 = 3 м, l2 = 1 м.

139. Определить прогиб точки приложения силы стального бруса квадратного 2020 мм сечения, если Р = 20 кН, l1 = l2 = 1 м.

140. Определить угол поворота левого опорного сечения стального бруса квадратного 2020 мм сечения, если Р = 15 кН, l1 = l2 = 2 м.

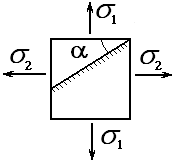
141. Определить энергию изменения объема для элементарного кубика, выделенного из стальной детали, находящегося в объемном напряженном состоянии, если главные напряжения равны 100 МПа, 70 МПа и 40 МПа соответственно.

142. Определить наибольшую по абсолютной величине относительную деформацию для стального элемента, находящегося в объемном напряженном состоянии, если главные напряжения составляют + 15 МПа, + 30 МПа и + 45 МПа соответственно.

143. Определить угол поворота левого опорного сечения стального бруса квадратного 3030 мм сечения, если M = 40 кНм, l1 = 3 м, l2 = 2 м.

144. Используя теорему Кастилиано, найти угол поворота свободного конца стальной балки. Дано: М = 1 кНм, l =2 м, сечение двутавр № 12.

145. Определить угол поворота концевого сечения стального бруса квадратного 2020 мм сечения, если M = 40 кНм, l = 4 м.

последние

146. Напишите условия прочности и жесткости при кручении.

147.Из расчета на жесткость определить потребный диаметр вала для передачи мощности 63 кВт при скорости 30 рад/с. Материал вала – сталь, модуль упругости при сдвиге G =МПа, допускаемый относительный угол закручивания 0,02 рад/м.

148. Сплошной вал круглого сечения был запроектирован в предположении определенной скорости его вращения. Затем было решено повысить скорость в 20 раз. Как изменился диаметр вала после пересчета его при неизменных остальных данных?

149. При испытании на кручение стального цилиндрического образца оказалось, что возрастание крутящего момента на 5 Hм вызывает приращение угла закручивания на 0,002 рад на длине 20 см. Вычислить модуль сдвига материала образца G и коэффициент Пуассона , если известны модуль упругости при растяжении Е= =2 *10**5 МПа и диаметр образца d=16 мм.

150. Поясните смысл предположения о сплошности среды.

151. Что характеризуют диагональные и недиагональные компоненты тензора деформации?

152. Почему коэффициент Пуассона для реальных тел не может быть больше 0,5?

153. Какие деформации называют упругими?

154. Что характеризует след тензора деформации?

155. Найти главные значения тензора напряжений

156. Определите наружный диаметр полого вала D (внутренний диаметр составляет 50% от наружного), равнопрочного сплошному валу с диаметром 50 мм.

157. Определить энергию изменения объема для элементарного кубика, выделенного из стальной детали, находящегося в объемном напряженном состоянии, если главные напряжения равны 100 МПа, 70 МПа и 40 МПа соответственно.

158. Охарактеризуйте тензор деформаций (ранг, симметричность или антисимметричность, физический смысл компонент).

159. Как выглядит взаимосвязь плотности и объемной деформации индивидуальной частицы сплошной среды?

160. На грани элементарного кубика, вырезанного из стального ствола орудия, действуют нормальные напряжения: 450 МПа, 120 МПа и 250 МПа. Определить наибольшее касательное напряжение.

161. По заданным 100 МПа и 50 МПа (плоское напряженное состояние) определить напряжения в сечении под углом . Определить наибольшие касательные напряжения в элементе.

162. Определить нормальное и касательное напряжения по наклонному ( ) сечению в элементе, по граням которого известны нормальные и касательные напряжения. Дано: 80 МПа, 0, 40 МПа.

163. По заданным 40 МПа, 20 МПа и = 10 МПа () определить величину и направление главных напряжений и изобразить элемент, находящийся под действием только одних главных напряжений.

164. Определить диаметры полого стального вала, передающего мощность 7000 кВт при 100 об/мин, если наибольшее касательное напряжение в вале 60 МПа, а внутренний диаметр составляет 0,6 от наружного.

165. Какой максимальный крутящий момент может быть приложен к валу с диаметром 65 мм, если допускаемое напряжение для материала вала 50 МПа?

165. Найдите изменение размеров бруса (длины, ширины, толщины), если сечение квадратное 10x10 см2, коэффициент Пуассона . Линей­ный участок диаграммы растяжения материала представлен на рисунке.

166. Определить тензор напряжений в опасной точке длинного стержня, стоящего вертикально в однородном поле тяжести.

167. Что характеризуют диагональные и недиагональные компоненты тензора напряжений?

168. Хрупкий материал испытали на сжатие и получили предел прочности σ_вс. Достаточно ли этого для расчёта конструкции, работающей на изгиб? Обоснуйте ваше заключение.

169. С чем связана возможность введения такой идеализации реальной деформируемой среды, как сплошная среда?

13