§1. Матрицы

1О. Основные определения.

Определение 1. Матрицей размеров над множеством действительных чисел R называется прямоугольная таблица из вещественных чисел, имеющая строк и столбцов:

,

где R, – номер строки, – номер столбца, − элементы матрицы, и − порядки матрицы. В этом случае говорят, что рассматриваемая матрица размера . Если , то матрица называется квадратной, а число – её порядком.

Для изображения матрицы применяются либо круглые скобки, либо сдвоенные прямые:

или .

Для краткого обозначения матрицы используются либо заглавные латинские буквы ; либо символы , , указывающее обозначение элементов матрицы; либо используется запись .

Множество всех матриц размера обозначается R R.

Частные случаи матриц.

1. Если , то матрица называется квадратной. Её диагональ называется главной диагональю, а – побочной диагональю.

2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е. .

3. Диагональная матрица вида называется скалярной.

4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается или , где – ее порядок.

5. Матрица размера , у которой все элементы равны нулю, называется нулевой и обозначается .

6. Если , то матрица называется строчной, или матрица-строка, или строка. Если столбцовая = матрица-столбец = столбец.

Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.

2^о. Операции над матрицами и их свойства.

Определение 3. Суммой матриц и R (т.е. имеющих одинаковые порядки) называется матрица R: .

Обозначение: .

Пример.

.

Свойства (сложения матриц).

1) Коммутативность сложения, т.е., R справедливо .

2) Ассоциативность сложения, т.е., R справедливо .

3) R.

4) R!R. При этом, если , то . Матрица называется противоположной к и обозначается .

Доказательство свойств провести самостоятельно прямыми вычислениями.

Определение 4. Произведением элемента R на матрицу R называется матрица R

Обозначение: .

Операция, сопоставляющая и их произведение называется умножением числа на матрицу.

Свойства (умножения матрицы на число).

R, Rвыполняется

1) ,

2) ,

3) ,

4) .

Доказательство свойств – самостоятельно прямыми вычислениями.

Замечание. Разность двух прямоугольных матриц и R определяется равенством .

Определение 5. Произведением матриц размера и размера называется матрица размеров такая, что каждый элемент .

Обозначение: .

Операция произведения на называется умножением этих матриц.

Из определения следует, что элемент матрицы , стоящий в –ой строке и –ом столбце, равен сумме произведений элементов –ой строки матрицы на –ый столбец матрицы .

Примеры.

1) ,

2) .

Таким образом, две матрицы можно перемножать, если число столбцов матрицы равно числу строк матрицы . Тогда матрица называется согласованной с . Из согласованности с не следует согласованность с . Если даже условие согласования выполняется, то в общем случае .

Свойства (умножения матриц).

1) Ассоциативность умножения матриц, т.е.,R,R R справедливо .

Доказательство. Из определения 5 следует, что элемент матрицы равен , а элемент матрицы равен . Равенство следует из возможности изменения порядка суммирования.

2) Дистрибутивность сложения относительно умножения, т.е.,

, R R .

, R, R.

Доказательство следует из определения суммы и произведения матриц.

3) R.

Доказательство. Пусть, и . Тогда . Здесь – символ Кронекера.

.

4) R R.

5) R ,.

Доказательство свойств 4)-5) проводится аналогично свойству 3).

6) R R, R .

Замечание. В общем случае произведение матриц не коммутативно. Например,

.

Но из свойств 4) и 5) умножение квадратной матрицы на и коммутирует. Также коммутирует умножение квадратной матрицы на скалярную.

3^о. Блочные матрицы.

Пусть матрица при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых является матрицей меньших размеров и называется блоком исходной матрицы. В этом случае рассматривается как некоторая новая, блочная матрица , элементами которой являются блоки указанной матрицы ( – элементы матрицы, поэтому заглавное). Здесь – номер блочной строки, – столбца. Например, если

, то ,

, , .

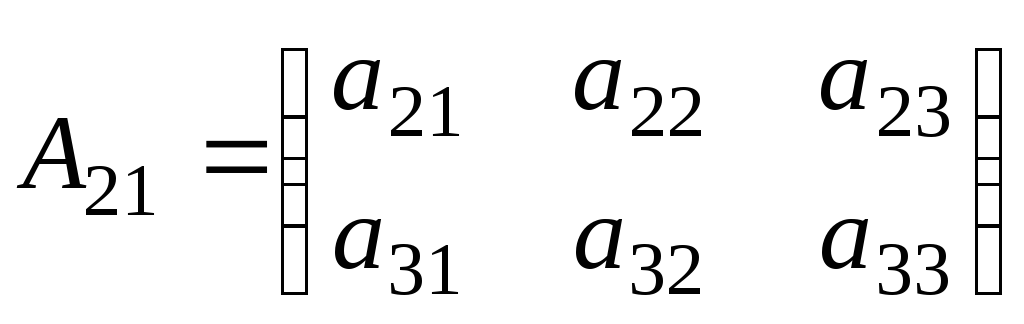Замечательным является факт, что операции с блочными матрицами совершаются по тем же правилам, что и обычными, только в роли элементов выступают блоки. Действительно, если , то , где вычисляется по обычному правилу умножения матрицы на число. Аналогично, если и имеют одинаковые порядки и одинаковым образом разбиты на блоки, то сумме отвечает блочная матрица : .

Для умножения R на R необходимо согласовать их разбиение на блоки, т.е. число столбцов каждого блока должно быть равно числу строк блока . Тогда .

Для доказательства необходимо расписать правую и левую части в терминах обычных элементов матриц . Пусть разбиение матриц проведено следующим образом:

.

Если , то и , откуда следует, что

, что и требовалось доказать.

Пример. Пусть 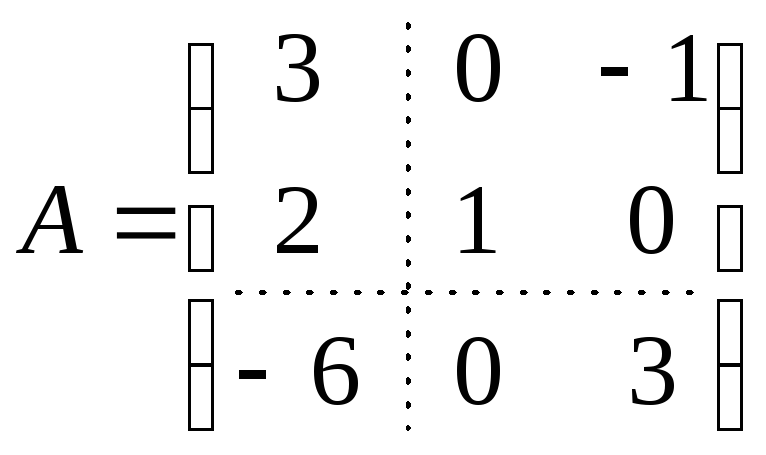, , 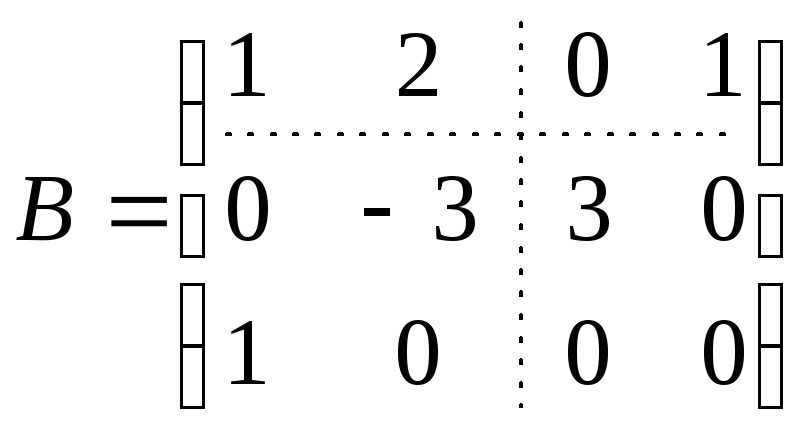т.е.

, ,

где

,

.

Тогда . Аналогично находятся остальные . В результате получаем

.

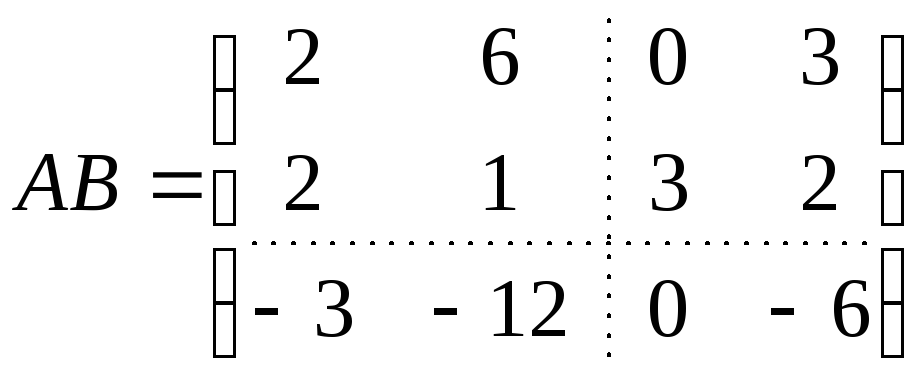В качестве применения блочных матриц рассмотрим

Определение 6. Прямой суммой квадратных матриц порядков соответственно называется квадратная матрица порядка : .

Обозначение: .