
- •§14. Линии второго порядка
- •1°. Определение эллипса, каноническое уравнение эллипса, исследование формы эллипса.
- •2°. Определение гиперболы, каноническое уравнение гиперболы, исследование формы гиперболы.
- •3°. Определение параболы, каноническое уравнение, исследование формы.
- •4°. Директрисы эллипса и гиперболы.
- •6°. Исследование общего уравнения второго порядка.
3°. Определение параболы, каноническое уравнение, исследование формы.
Пусть на плоскости
заданы точка
![]() и прямая
и прямая
![]() ,
не проходящая через эту точку.
,
не проходящая через эту точку.
Определение 5.
Параболой
называется множество точек плоскости,
каждая из которых равноудалена от точки
![]() и прямой
и прямой
![]() .
Точка
.
Точка
![]() называется фокусом
параболы,
прямая
называется фокусом
параболы,
прямая
![]() – директрисой
параболы.
– директрисой
параболы.

Рис. 5
Составим уравнение
параболы. Выберем прямоугольную систему
координат так, что ось
![]() проходит через фокус
проходит через фокус
![]() перпендикулярно к директрисе
перпендикулярно к директрисе
![]() в направлении от директрисы
в направлении от директрисы
![]() к фокусу
к фокусу
![]() .
Начало координат возьмём в середине
отрезка между фокусом
.
Начало координат возьмём в середине
отрезка между фокусом
![]() и точкой пересечения оси
и точкой пересечения оси
![]() с директрисой
с директрисой
![]() .
Пусть расстояние между фокусом и
директрисой (фокальный
параметр):
тогда
.
Пусть расстояние между фокусом и
директрисой (фокальный
параметр):
тогда
![]() и уравнение директрисы
и уравнение директрисы
![]() будет иметь вид
будет иметь вид
![]() .
.
Пусть
![]() – произвольная точка параболы. Обозначим
через
– произвольная точка параболы. Обозначим
через
![]() и назовём фокальным
радиусом
точки
и назовём фокальным
радиусом
точки
![]() расстояние от
расстояние от
![]() до фокуса
до фокуса
![]() .
Расстояние от точки
.
Расстояние от точки
![]() до директрисы обозначим
до директрисы обозначим
![]() .
Согласно определению параболы равенство
.
Согласно определению параболы равенство
![]()
является необходимым
и достаточным условием принадлежности
точки
![]() данной параболе. Так как
данной параболе. Так как
![]()
![]() ,
,
то соотношение
![]() (16)
(16)
представляет собой уравнение параболы в выбранной системе координат.
Возводя обе части равенства (16) в квадрат, получаем
![]() ,
,
откуда
![]() .
(17)
.
(17)
Покажем обратное:
если координаты
![]() точки
точки
![]() удовлетворяют уравнению (17), то точка
удовлетворяют уравнению (17), то точка
![]() лежит на параболе. Действительно, из
(17) следует, что
лежит на параболе. Действительно, из
(17) следует, что
![]() .
Тогда
.
Тогда
![]() .
Используя это, получаем
.
Используя это, получаем
![]() .
.
Таким образом, для
того чтобы точка
![]() с координатами
с координатами
![]() принадлежала параболе, необходимо и
достаточно, чтобы её координаты
удовлетворяли уравнению (17). Уравнение
(17) называется каноническим
уравнением параболы.
принадлежала параболе, необходимо и
достаточно, чтобы её координаты
удовлетворяли уравнению (17). Уравнение
(17) называется каноническим
уравнением параболы.
Итак, для точки
![]() параболы выполняется
параболы выполняется
![]() .
Так как для точек эллипса и гиперболы
отношение
.
Так как для точек эллипса и гиперболы
отношение
![]() ,
то для параболы естественно положить
эксцентриситет
,
то для параболы естественно положить
эксцентриситет
![]() равным единице.
равным единице.
Из уравнения (17)
видно, что все точки параболы лежат в
первой и четвёртой четвертях. Ввиду
того, что уравнение (17) содержит координату
![]() только в чётной степени, то парабола
симметрична относительно оси
только в чётной степени, то парабола
симметрична относительно оси
![]() ,
и поэтому достаточно исследовать её
форму в первой координатной четверти.
В этой четверти рассматриваемая парабола
описывается уравнением
,
и поэтому достаточно исследовать её
форму в первой координатной четверти.
В этой четверти рассматриваемая парабола
описывается уравнением
![]() .
Функция
.
Функция
![]() является монотонно возрастающей,
выпуклой вверх, так как
является монотонно возрастающей,
выпуклой вверх, так как
![]() ,
,
![]() .
.
Наклонных асимптот
вида
![]() для графика функций
для графика функций
![]() в первой четверти нет (следовательно,
нет их и для графика функции
в первой четверти нет (следовательно,
нет их и для графика функции
![]() в четвёртой четверти), поскольку иначе
в четвёртой четверти), поскольку иначе
![]() ,
,
![]() .
.
У параболы нет
вертикальных асимптот, так как функция
![]() непрерывна на
непрерывна на
![]() .
Таким образом, парабола имеет, изображённый
на рис. 6.
.
Таким образом, парабола имеет, изображённый
на рис. 6.
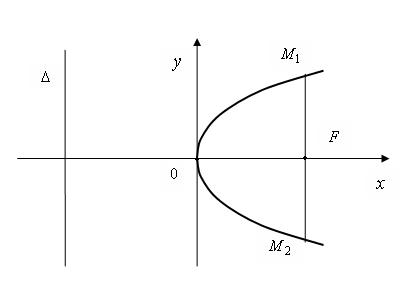
Рис. 6
Ось симметрии параболы называется её осью. Точка пересечения параболы с её осью называется вершиной параболы.
Укажем теперь
геометрический смысл фокального
параметра
![]() .
Для этого через фокус
.
Для этого через фокус
![]() проведём прямую, перпендикулярную к
оси параболы (см. рис. 6). Уравнение этой
прямой имеет вид
проведём прямую, перпендикулярную к
оси параболы (см. рис. 6). Уравнение этой
прямой имеет вид
![]() .
Найдём координаты точек
.
Найдём координаты точек
![]() пересечения прямой
пересечения прямой
![]() с параболой:
с параболой:

Следовательно,
![]() ,
,
![]() ,
,
![]() .
.
Итак, фокальный
параметр
![]() параболы равен длине перпендикуляра к
оси параболы, восстановленного из фокуса
до точки пересечения с параболой. В этом
смысле фокальный параметр
параболы равен длине перпендикуляра к
оси параболы, восстановленного из фокуса
до точки пересечения с параболой. В этом
смысле фокальный параметр
![]() характеризует форму параболы.
характеризует форму параболы.
