Пример 1. Задача оптимального использования ресурсов

Фабрика имеет в своём распоряжении определённое количество ресурсов: рабочую силу, деньги, сырьё, оборудование, производственные площади и т.п. Допустим, например, ресурсы трёх видов: рабочая сила, сырьё и оборудование – имеются в количестве соответственно 80 (чел/дней), 480 (кг) и 130 (станко/ч). Фабрика может выпускать ковры четырёх видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице.

Ресурсы	Нормы расхода ресурсов на единицу изделия				Наличие ресурсов
	ковёр «Лужайка»	ковёр «Силуэт»	ковёр «Детский»	ковёр «Дымка»
Труд	7	2	2	6	80
Сырьё	5	8	4	3	480
Оборудование	2	4	1	8	130
Цена (тыс. руб.)	3	4	3	1

Требуется найти такой план выпуска продукции, при котором будет максимальная общая стоимость продукции.

Обозначим через Х₁, Х₂, Х₃, Х₄ количество ковров каждого типа.

Экономико-математическая модель задачи.

Целевая функция – это выражение, которое необходимо максимизировать:

→max

Ограничения по ресурсам

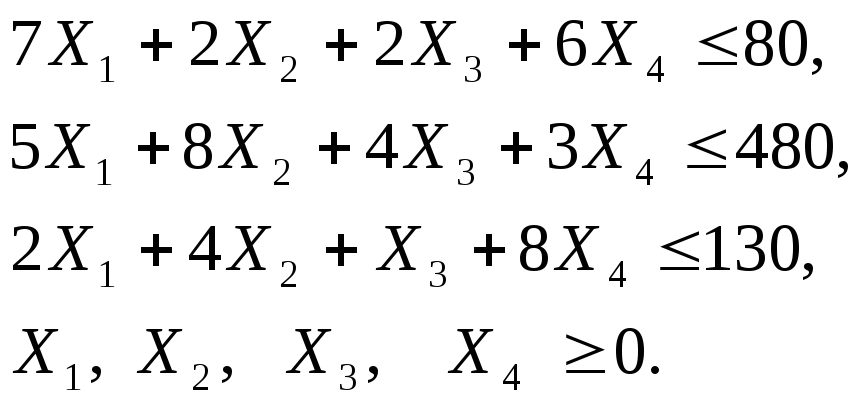
Технология решения задач линейного программирования с помощью Поиска решений в среде ms Excel.

Одним из способов численного решения задач линейного программирования является использование надстройки «Поиск решения» электронных таблиц Microsoft Excel. В частности, «Поиск решения» предоставляет возможность:

1. использования планов большой размерности (т. е. с большим количеством варьируемых переменных);

2. задания ограничений сложного вида;

3. отыскания оптимального из допустимых решений;

4. генерирования множества различных решений, сохраняемых в дальнейшем в виде сценариев;

5. автоматического создания отчета по решению задачи.

Теоретической основой надстройки «Поиск решения» является симплекс-метод, позволяющий находить оптимальное решение задачи планирования с помощью итерационного процесса перехода к улучшающимся планам.

Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервис → Надстройки и активизируйте надстройку Поиск решения. Если же этой надстройки нет в диалоговом окне Надстройки, то вам необходимо обратиться у панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки Excel (или Office) установить надстройку Поиск решения.

После выбора команд Сервис  Поиск решения появится диалоговое окно Поиск решения.

Для решения задачи необходимо:

1. Создать форму для ввода условий задачи.

2. Указать адреса ячеек, в которые будет помещён результат решения (изменяемые ячейки).

3. Ввести исходные данные.

4. Ввести зависимость для целевой функции.

5. Ввести зависимости для ограничений.

6. Указать назначение целевой функции (установить целевую ячейку).

7. Ввести ограничения.

8. Ввести параметры для решения ЗЛП.

Рассмотрим на Примере 1 технологию решения Задачи оптимального использования ресурсов.

1. Подготовим форму для ввода условий ( см. рис.1).

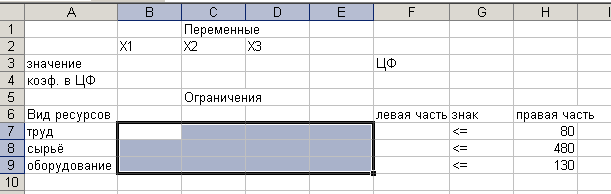
Рис.1. Введена форма для ввода данных.

2. В нашей задаче оптимальные значения вектора Х=(Х1, Х2, Х3, Х4) будут помещены в ячейках В3:Е3, оптимальное значение целевой функции – в ячейке F4.

3. Введём исходные данные в созданную форму. Получим результат, показанный на рис. 2.

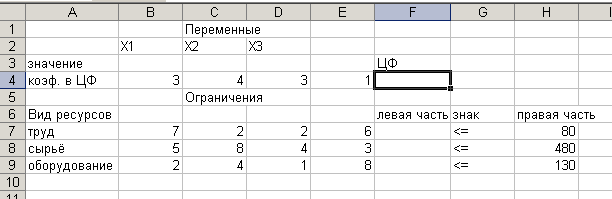
Рис.2. Данные введены.

4. Введём зависимость для целевой функции:

• Курсор в F4

• Нажать кнопку Мастер функций f_x на панели инструментов Стандартная.

• На экране появится диалоговое окно Мастер функций шаг 1 из 2.

• Выбрать категорию Математические.

• Выбрать функцию СУММПРОИЗВ.

• В массив 1 ввести B$3:E$3.

• В массив 2 ввести B4:E4.

• Готово. На экране: в F4 введена функция, как показано на рис. 3.

5. Введём зависимость для левых частей ограничений:

• Курсор в F4.

• Копировать в буфер.

• Выделить блок F7:F9.

• Вставить из буфера.

На этом ввод зависимостей закончен.

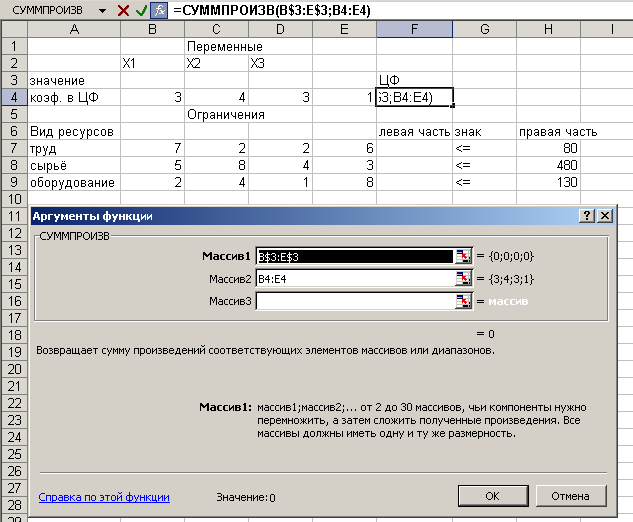
Рис.3. Вводится функция для вычисления целевой функции.