
- •2.1. Раскрытие статической неопределимости.
- •2.1.2. Выбор основной и эквивалентной систем
- •2.1.2. Составление системы канонических уравнений метода сил
- •2.1.3. Построение единичных и грузовых эпюр
- •2.1.4. Определение коэффициентов канонических уравнений
- •2.1.5. Построение суммарной эпюры изгибающих моментов
- •2.2. Проверка раскрытия статической неопределимости.
- •2.2.1. Кинематическая проверка
- •2.2.2. Построение эпюр перерезающих и нормальных сил
- •2.2.3. Статическая проверка
- •2.3. Расчет на прочность по нормальным напряжениям изгиба
2.2.2. Построение эпюр перерезающих и нормальных сил
Определим реакции в опорах в эквивалентной системе. Для этого запишем уравнения статистического равновесия.
∑ прX Fi = 0; RDX + X1 – P = 0; RDX = P – X1 = 14 – 10,9 = 3,1 кН
RDX = 3,1 кН
∑ прY Fi = 0; RDX + X2 – q . l = 0; RDY = ql – X2 = 5 . 2,4 – 7,44 = 4,56 кН
RDY = 4,56 кН.
∑ momD Fi = 0;
– MD
+ P
.
l
– ql
.
![]() – M
– X1
(l
– kl)
+ X2
.
l
= 0.
– M
– X1
(l
– kl)
+ X2
.
l
= 0.
МD
= P .
l –
![]() – M – X1
(l – kl) + X2
.
l
= 14 .
2,4 – 5 .
– M – X1
(l – kl) + X2
.
l
= 14 .
2,4 – 5 .
![]() – 22 –
– 22 –
10,9 (2,4 – 1,44) + 7,44 . 2,4 = 4,64 кНм.
Запишем функцию N(z1) и Q∑ (z1) на расчетных участках (рис.2.2, б).
Участок AB; 0 ≤ z1 ≤ 1,44 м.
N∑ (z1) = – X2 = 7,44 кН; Q∑ = X1 = 10,9 кН.
Участок BC; 0 ≤ z2 ≤ l=2,4м.
N∑ (z 2) = X1 = 10,9 кН;
Q∑
(Z2)
= q
.
z2
– X2
=
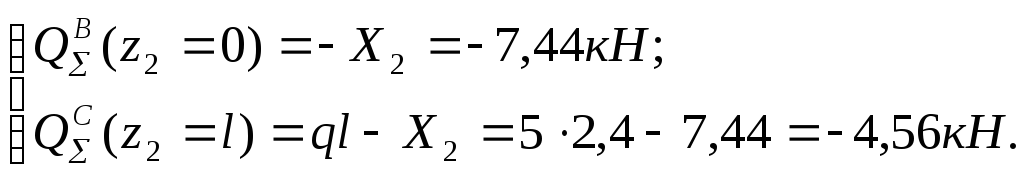
Участок CD; 0 ≤ z3 ≤ l = 2,4 м.
N∑ (z3) = X2 – ql = 7,44 – 5 . 2,4 = – 4,56 кН;
Q∑ (z3) = X1 – P = 10,9 – 14 = – 3,1 кН.
По полученным данным строим эпюры ЭN∑ (рис.2.4, а) и ЭQ∑ (рис.2.4, б).
-

а
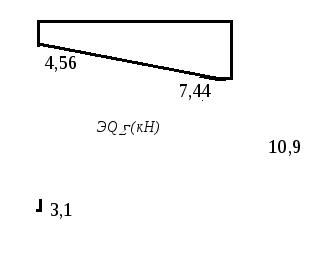
б
Рис.2.4
2.2.3. Статическая проверка
-
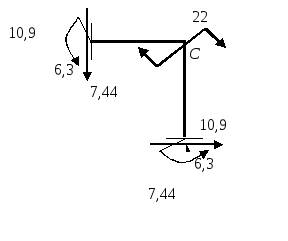
Рис. 2.5
Рассмотрим равновесие, например, в узле B. Проверим равновесии по уравнению моментов относительно центра узла (рис.2.5).
∑ momC Fi = 9,2 + 15,9 + 6,3 = 0
Следовательно, узел B находится в равновесии.
Выполненных проверок достаточно, чтобы убедиться в правильности решение задачи.
2.3. Расчет на прочность по нормальным напряжениям изгиба
В соответствии с заданием необходимо подобрать номер профиля (двутавр) из условия прочности в опасном сечении по нормальным напряжениям изгиба.
Опасным является сечение B, принадлежащее участку AB, в котором изгибающей момент M∑ max = 15,9 кН.м наибольший.
Запишем условие прочности
σ max
=
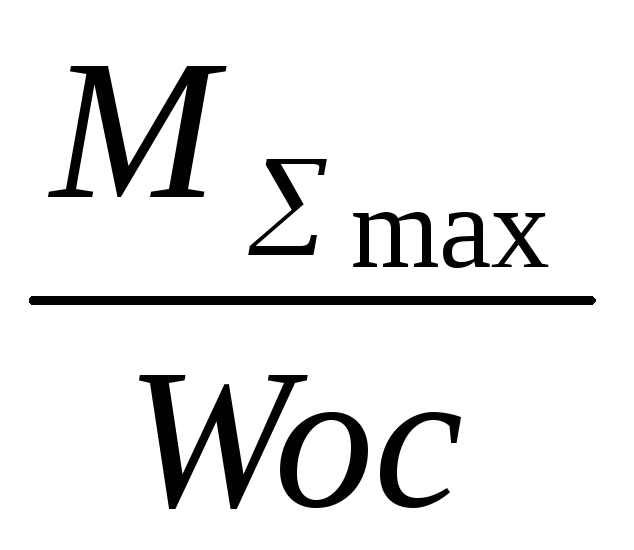 ≤ [σ],
≤ [σ],
где [σ]
=
![]() – допускаемое напряжение;σT
– предел текучести материала, n
– коэффициент запаса.
– допускаемое напряжение;σT
– предел текучести материала, n
– коэффициент запаса.
Для стали З σT =210 МПа, коэффициент запаса примем n = 1,5, тогда
[σ]
=
![]() =
=![]() = 160 МПа.
= 160 МПа.
Из условия прочности
Wxрасч.
=
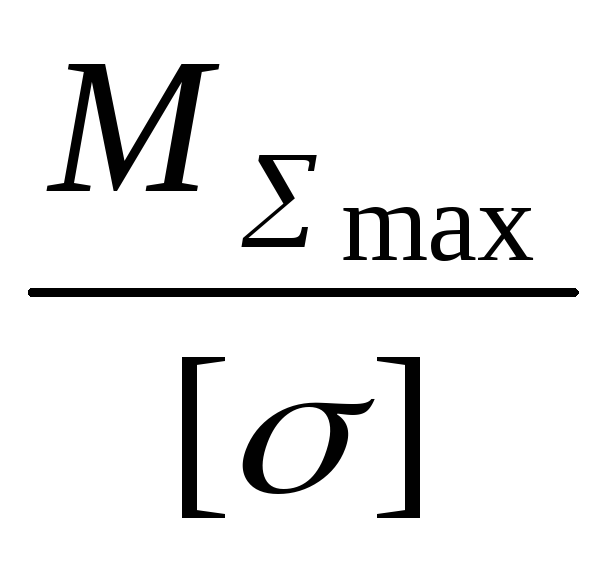 =
=![]() = 95210 мм3
= 95,2см3.
= 95210 мм3
= 95,2см3.
По таблице
сортаментов (гост
8239-72) выбираем двутавр № 16 (W![]() = 109 см3).
При этом наибольшие напряжения σmax.
на внешних волокнах будут равны
= 109 см3).
При этом наибольшие напряжения σmax.
на внешних волокнах будут равны
σmax
=
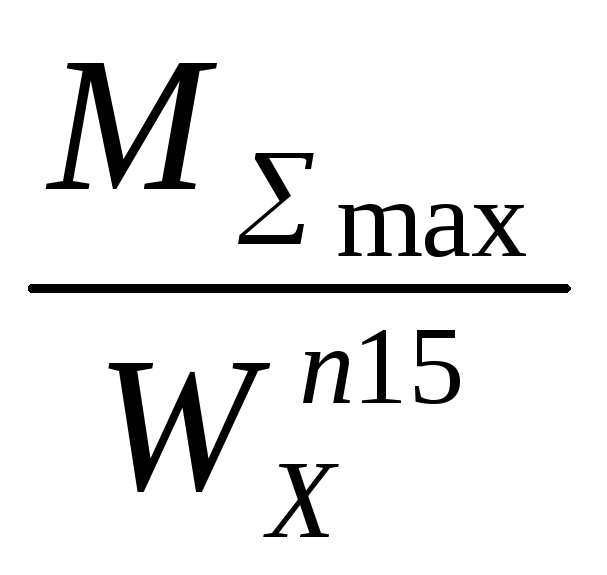 =
=
![]() = 146 МПа.
= 146 МПа.
Ошибка подбора (недогрузка)
∆σ =
![]() .
.
![]() .
100% = 8,75%,
.
100% = 8,75%,
что вполне допустимо.
Список литературы
Феодосьев В.И. Сопротивление материалов: учебник для ВУЗов. – М.: Наука, 1986. – 560с.
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов: учебник для ВУЗов. – М.: Изд-во МАИ, 1994. – 512с.
Справочник по сопротивлению материалов / Писаренко Г.С. и др. – Киев: Наукова думка, 1988. – 736с.
Справочник по сопротивлению материалов / Рудицын М.Н., Артемов П.Я., Любошиц М.И. – Минск: Вышэйшая школа, 1970. – 630с.
Серенсен С.В., Кокаев В.П., Шнейдерович Р.М. Валы и оси. М.: Машиностроение, 1970.
Анурьев В.И. Справочник конструктора – машиностроителя: в 3-х т. Т.1. – 5-е изд., перераб. И доп. – М.: Машиностроение, 1978. – 728с.
Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. М.: Машиностроение, 1985. – 564с.
