
- •51. Амплитудно-импульсная модуляция. Спектр аим - колебаний. Почему она применена в представленной схеме уравновешивания?
- •Рве 2.28. Импульсная модуляция: а — периодическая последовательность исходных импульсов; б—модулирующий сигнал; в — аим; г — шим; д — фим; е — икм
- •52. Частотное и временное разделение каналов.
- •53. Фильтрация сигналов. Операторы фильтрации.
- •54. Вероятность и информация. Информационное содержание сигнала.
- •55. Энтропия, количество информации по Шеннону.
- •56. Описание непрерывных колебаний во временной и частотной областях.
- •57. Базисные функции. Ортогональные и ортонормированные функции.
- •58. Спектральная плотность случайных колебаний. “Белый шум” и его свойства.
- •59. Случайные колебания и корреляционные функции.
- •60. Способы повышения помехоустойчивости передачи информации.
- •61. Корреляционное разделение каналов и корреляционная фильтрация.
- •62. Демодуляция частотно – модулированных колебаний.
- •63. Виды каналов передачи информации.
- •64. Информация и фазы обращения информации.
- •65. Виды информации. Устранение избыточности информации.
- •66. Структурные меры информации.
- •67. Статистические меры информации. Информационное содержание сигнала.
- •68. Частотная модуляция. Спектры чм – колебаний.
- •69. Какие виды модуляции гармонических колебаний можно обнаружить в радиокомпасе и каковы их спектры?
- •70. Модуляция гармонических колебаний. Виды амплитудной модуляции и как они представлены в арк?
- •71. Дискретизация сигналов. Теорема Котельникова.
- •72. Систематические (семантические) меры информации. Источники и приемники информации.
- •73. Геометрические меры информации. Каким образом они представлены в индикаторах сои?
- •74. Количество информации. Аддитивные меры Хартли.
- •75. Импульсная модуляция, шим, спектр широтно-импульсных колебаний.
51. Амплитудно-импульсная модуляция. Спектр аим - колебаний. Почему она применена в представленной схеме уравновешивания?
При импульсной модуляции (рис. 2.28) в качестве несущего колебания (точнее, поднесущего) используются различные периодические импульсные последовательности, в один из параметров которых вводится информация о передаваемом сообщении. Для дискретных сигналов процесс модуляции принято называть манипуляцией параметров импульсов.
Положим,
что поднесущим колебанием в системе
передачи информации с импульсной
модуляцией является периодическая
последовательность прямоугольных
импульсов с амплитудой![]() ,
длительностью
,
длительностью![]() и
периодом повторения Г (рис. 2.28,а).
Для наглядности
и упрощения выкладок выберем в качестве
модулирующего сигнала гармоническое
колебание вида (2.57) с начальной фазой
и
периодом повторения Г (рис. 2.28,а).
Для наглядности
и упрощения выкладок выберем в качестве
модулирующего сигнала гармоническое
колебание вида (2.57) с начальной фазой![]() =
90° (рис. 2.28, б).
=
90° (рис. 2.28, б).


Рве 2.28. Импульсная модуляция: а — периодическая последовательность исходных импульсов; б—модулирующий сигнал; в — аим; г — шим; д — фим; е — икм
В качестве примера, позволяющего оценить параметры импульсно-модулированных колебаний, рассмотрим АИМ-сигнал и определим его спектр при модуляции импульсной последовательности гармоническим колебанием
![]()
Представим
периодическую последовательность
прямоугольных немодулированных
импульсов![]() с
амплитудой
с
амплитудой![]() тригонометрическим
рядом Фурье (2.12). Введем в формулу (2.59)
вместо несущего колебания
тригонометрическим
рядом Фурье (2.12). Введем в формулу (2.59)
вместо несущего колебания![]()
![]() функцию
функцию![]() ,
описывающую последовательность
прямоугольных импульсов. Тогда АИМ-сигнал
можно записать в виде
,
описывающую последовательность
прямоугольных импульсов. Тогда АИМ-сигнал
можно записать в виде
![]() (2.85)
(2.85)

Рис. 2.29. Спектр сигнала при амплитудно-импульсной модуляции
В
этом соотношении параметр![]() —
коэффициент (глубина) модуляции импульсов.
Подставляя значение
—
коэффициент (глубина) модуляции импульсов.
Подставляя значение![]() из
(2.13) в (2.85), после несложных преобразований,
запишем выражение для АИМ-сигнала:
из
(2.13) в (2.85), после несложных преобразований,
запишем выражение для АИМ-сигнала:
![]()
![]()
![]() (2.86)
(2.86)
Из
формулы (2.86) следует, что при однотональной
амплитудно-импульсной модуляции (рис.
2.29) периодической последовательности
прямоугольных импульсов спектр
полученного сигнала содержит постоянную
составляющую![]() ,
гармонику
,
гармонику![]() частоты модуляции
частоты модуляции![]() и
высшие гармонические составляющие
и
высшие гармонические составляющие![]() частоты
следования импульсов
частоты
следования импульсов![]() ,
около каждой из которых симметрично
расположены боковые составляющие с
частотами
,
около каждой из которых симметрично
расположены боковые составляющие с
частотами![]()
52. Частотное и временное разделение каналов.
Разделение каналов.
В линии связи поступает составной сигнал (спектр гармонических составляющих сигналов), представляющий собой сумму сигналов отдельных каналов.
![]()
Процесс разделения можно рассматривать как фильтрацию осуществляющих выделение отдельных каналов
![]()
Фк – алгоритм выделения (оператор фильтрации).
В зависимости от вида Фк различают методы разделения каналов:
- пространственные;
- частотные;
- временные;
- фазовые;
- корреляционные;
… и т.д.
При временном разделении принципиально возможны как асинхронный, так и синхронный режимы работы. В системах связи с большим числом каналов обычно применяется синхронный режим работы, позволяющий обеспечить минимум переходных помех в системе, т.е. временное разделение каналов сигнала от каждого датчика передаётся только в отведённое для них непосредственно не пересекающиеся отрезки времени ∆t.

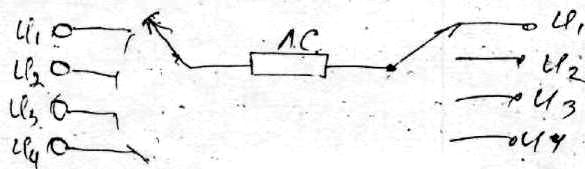
На базе частотных разделения каналов работают приёмники и телевизоры.
При
частотном разделении для
передачи информации в каждом стволе
используется определенная несущая
частота —![]()
![]() (рис. 4-31, а). Защитный промежуток по
частоте
(рис. 4-31, а). Защитный промежуток по
частоте![]() между
соседними станциями должен выбираться
из условия исключения взаимного
перекрытия спектров. При использовании
частотного разделения могут быть
применены любые виды передачи—
однополосная (ОБП), частотная (ЧМ),
кодово-импульсная модуляция (КИМ) и др.
Достоинства данного метода: возможность
асинхронной работы всей системы при
различном числе каналов в земных
станциях; простота сопряжения с
существующими системами наземной связи,
где широко используется частотное
уплотнение каналов. Недостатки:
необходимость регулировки мощности
земных станций с целью исключения
подавления слабых сигналов сильными
при воздействии их на нелинейный элемент
ретранслятора; невысокая эффективность
использования мощности ретранслятора.
между
соседними станциями должен выбираться
из условия исключения взаимного
перекрытия спектров. При использовании
частотного разделения могут быть
применены любые виды передачи—
однополосная (ОБП), частотная (ЧМ),
кодово-импульсная модуляция (КИМ) и др.
Достоинства данного метода: возможность
асинхронной работы всей системы при
различном числе каналов в земных
станциях; простота сопряжения с
существующими системами наземной связи,
где широко используется частотное
уплотнение каналов. Недостатки:
необходимость регулировки мощности
земных станций с целью исключения
подавления слабых сигналов сильными
при воздействии их на нелинейный элемент
ретранслятора; невысокая эффективность
использования мощности ретранслятора.


Рис.4.31
Дм
– демодулятор; ЛС – линия связи;
![]() - частотное мультиплексирование;
- частотное мультиплексирование;
