15) Элементарная струйка, поток жидкости, живое сечение. Гидравлический радиус, расход и средняя скорость.

Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. Поток Ж – представляет собой совокупность элементарных струек.

Живым сечением – сечение потока Ж, перпендикулярное направлению скорости ее сечения. При плавно изменяющемся движении Ж сечение считается плоским и равным площади поперечного сечения потока ().

Площадь живого сечения S= dS

Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.

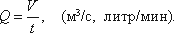
Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Гидравлический радиус потока R - отношение живого сечения к смоченному периметру Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками.

16) Уравнение неразрывности. Понятие расхода.

Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется.Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы. Пусть скорости стационарного течения жидкости через сечения трубы S₁ и S₂ равны соответственно v₁ и v₂. Объем жидкости, протекающей за промежуток времени t через сечение S₁, равен V₁=S₁v₁t, а объем жидкости, протекающей за то же время через сечение S2, равен V₂=S₂v₂t. Из равенства V₁=V₂ следует, что уравнением неразрывности. Из него следует, что Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.

Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Различают объёмный Q (м³/с), весовой Q_G(Н/с) и массовый Q_m(кг/с) расходы.

;

17) Распределение сил в сплошной среде. Объемные и поверхностные силы.

Внешние силы: массовые (объемные) и поверхностные.

Массовые силы в соответствии со вторым законом Ньютона про­порциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести и сила инерции переносного движения.

Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности.

Массо­вые силы относят к единице мас­сы, а поверхностные к единице площади

Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей.

Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой.

18) Уравнение Бернулли для установившегося движения жидкости.

Напорная линия – линия показывающая изменение гидродинамического напора Ж по длине потока

Линия, соединяющая уровни Ж в пьезометрах наз-ся пьезометрической линией

Отметим, что в такой записи члены уравнения выражают удельную энергию, отнесенную к весу (Mg = G).

Как и в гидростатике, величину z называют высотой положения, а величину p/gρ - пьезометрической высотой. 

Сумма первых двух членов уравнения  z + p/gρ - пьезометрический напор. 

Третий член уравнения u²/2g линейная величина. Как известно, начавшаяся двигаться вертикально со скоростью u при отсутствии сопротивления движению, поднялась бы на высоту u²/2g. Этот член уравнения Бернулли называется скоростной высотой или скоростным напором.