Лабораторная работа № 5. Метод простых итераций решения уравнения

Метод простых итераций (метод последовательных приближений) решения уравнения состоит в замене исходного уравнения эквивалентным ему уравнением и построении последовательности , сходящейся прик точному решению. Сформулируем достаточные условия сходимости метода простых итераций.

Теорема. Пусть функция определена и дифференцируема на, причём все её значения. Тогда, если существует число, такое, чтона отрезке, то последовательностьсходится к единственному нарешению уравненияпри любом начальном значении, т.е.

, , ,

При этом, если на отрезке производнаяположительна, то

,

если отрицательна, то

.

Опишем один шаг итераций. Исходя из найденного на предыдущем шаге значения , вычисляем. Если, полагаюти выполняют очередную итерацию. Если же, то вычисления заканчивают и за приближённое значение корня принимают величину. Погрешность полученного результата зависит от знака производнойкорень найден с погрешностью, если, то погрешность не превышает.

Метод допускает простую геометрическую интерпретацию. Построим графики функций и. Корнемуравнения

является абсцисса точки пересечения кривой с прямой(рис. 1). Взяв в качестве начальной произвольную точку, строим ломаную линию (рис.3 а, б). Абсциссы вершин этой ломанной представляют собой последовательные приближения корня. Из рисунков видно, что еслина отрезке, то последовательные приближенияколеблются около корня, если же производнаяположительна, то последовательные приближения сходятся к корню монотонно.

При использовании метода простых итераций основным моментом является выбор функции в уравнении, эквивалентном исходному. Для метода итераций следует подбирать функциютак, чтобы. При этом следует помнить, что скорость сходимости последовательностик корнютем выше, чем меньше число.

Пример. Найти корни уравнения с точностью.

Корни уравнения ,легко отделяются графически. Они являются абсциссами точек пересечения графикас прямой. Из приведенного (рис. 2) графика видно, что первый корень лежит на отрезке, а второй – на отрезке. Для определения первого корня заменим исходное уравнение эквивалентным; здесь,. На отрезке, т.е.. В качестве начального приближения выбираем. Вычисления прекращаем, когда. Последовательные приближения в этом случае таковы:

0,271828Е 00

0,131236Е 00

0,114024Е 00

0,112078Е 00

0,111860Е 00

0,111835Е 00

Так как

,

то принимаем . В этом результате все знаки верные.

Для определения второго корня представляем исходное уравнения в виде . Здесь,и припроизводнаяоценивается сверху:, т.е.. Если в качестве начального приближения взять, то получаем следующие последовательные приближения:

0,299573Е 01

0,339977Е 01

0,352629Е 01

0,356283Е 01

0,357314Е 01

0,357603Е 01

0,357684Е 01

0,357706Е 01

0,357713Е 01

Принимаем с погрешностью 0,0001, так как

.

Задание. Используя подпрограмму ЫШЕУК, найти корень уравнения с заданной точностью

Порядок выполнения лабораторной работы на ЭВМ.

1. Графически или аналитически отделить корень уравнения .

2. Преобразовать уравнение к видутак, чтобы в некоторой окрестностикорняпроизводнаяудовлетворяла условию. При этом следует помнить, что чем меньше, тем быстрее последовательные приближения сходятся к корню.

3. Выбрать начальное приближение, лежащее на отрезке .

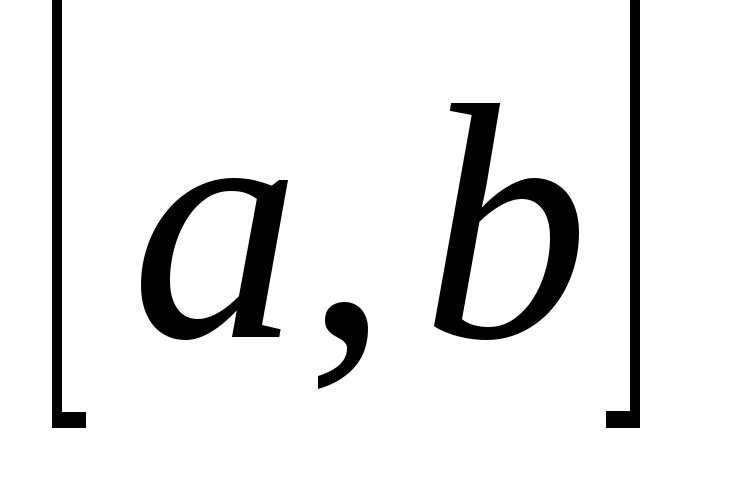4. Составить подпрограмму функцию для вычисления значений .

5. Составить головную программу и печать результатов вычислений.

6. Провести вычисления по программе.