
- •Введение
- •Лабораторная работа № 1. Решение системы линейных уравнений методом простых итераций и методом Чебышева Метод простых итераций
- •Метод Чебышева
- •Лабораторная работа № 2. Приближённое вычисление интеграла методом Симпсона
- •Порядок выполнения лабораторной работы на эвм.
- •Порядок выполнения лабораторной работы на эвм.
- •Порядок выполнения лабораторной работы на эвм.
- •Варианты заданий.
- •Лабораторная работа № 5. Метод простых итераций решения уравнения
- •0,271828Е 00
- •Варианты заданий.
- •Лабораторная работа № 6. Приближённое решение уравнения методом Ньютона
- •Порядок выполнения лабораторной работы на эвм.
- •Варианты заданий.
- •Лабораторная работа № 7. Решение системы нелинейных уравнений методом Ньютона
- •Порядок выполнения лабораторной работы на эвм.
- •Варианты заданий.
- •Лабораторная работа № 8. Приближённое решение задачи Коши методом Эйлера
- •Порядок выполнения лабораторной работы на эвм.
- •Варианты заданий.
- •Лабораторная работа № 9. Приближённое решение задачи Коши методом РунгеКутта
- •Порядок выполнения лабораторной работы на эвм.
- •Варианты заданий.
- •Лабораторная работа № 10. Решение задачи Дирихле для уравнения Пуассона методом Чебышева
- •Лабораторная работа № 11. Решение задачи Неймана для уравнения Пуассона методом скорейшего спуска
- •1. Постановка задачи
- •2. Теоретическая часть
- •3. Алгоритм
- •2. Задача Дирихле для уравнения Пуассона
- •3. Метод переменных направлений для уравнения Пуассона
- •5. Алгоритм решения задачи Дирихле для уравнения Пуассона
- •2) Прогонка в направлении оси
- •Прямой ход прогонки
- •Обратный ход прогонки
- •Прямой ход прогонки
- •3. Метод переменных направлений для задачи Дирихле
- •4. Алгоритм решения задачи Дирихле
- •Прямой ход прогонки
Лабораторная работа № 11. Решение задачи Неймана для уравнения Пуассона методом скорейшего спуска
1. Постановка задачи
Явным методом
Чебышева требуется приближенно решить
однородную задачу Неймана для уравнения
Пуассона в квадрате
![]() ,
которая состоит в следующем: найти
функцию
,
которая состоит в следующем: найти
функцию![]() ,
удовлетворяющую уравнению Пуассона и
краевым условиям
,
удовлетворяющую уравнению Пуассона и
краевым условиям
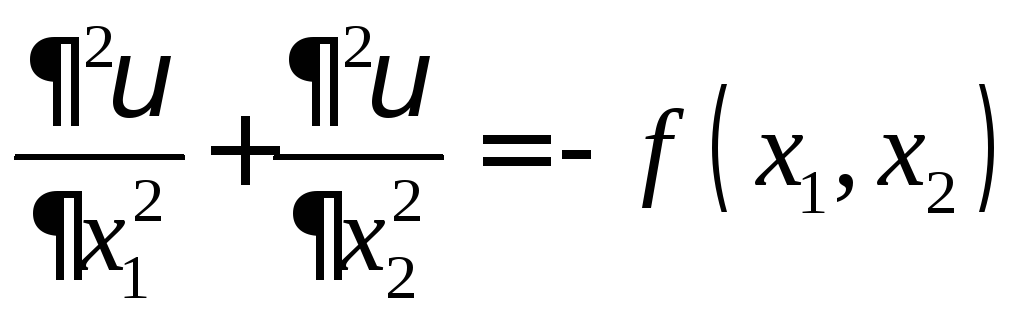 ,
(1)
,
(1)
![]() ,
(2)
,
(2)
где
![]() – граница квадрата
– граница квадрата![]() ,
,![]() – внешняя нормаль к
– внешняя нормаль к![]() .
.
Функция, удовлетворяющая краевым условиям (2)
![]() .
.
Вычислим
![]() .
.
Возьмём по определению в качестве правой части уравнения (1)
![]() .
.
2. Теоретическая часть
Для аппроксимации
производной в граничных условиях (2)
используем формулы второго порядка
точности через центральные разности.
Для этого вводим дополнительные точки
за пределами сеточной области
![]() .
Получаем:
.
Получаем:
![]() (3)
(3)
![]()
![]() .
.
На расширенной сетке аппроксимируем задачу (1), (2) в виде
![]() ,
,
![]() .
Пользуясь соотношениями (3), дополнительные
неизвестные
.
Пользуясь соотношениями (3), дополнительные
неизвестные
![]() исключаем. Тогда получим
исключаем. Тогда получим
![]() ,
,
![]() ,
,
![]() ,
,
|
|
(4) |
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Обозначим через
![]() пространство функций
пространство функций![]() ,
заданных на сетке
,
заданных на сетке![]() со скалярным произведением
со скалярным произведением
![]()
Сеточную функцию
![]() будем рассматривать как вектор с
координатами
будем рассматривать как вектор с
координатами![]() .
В пространстве
.
В пространстве![]() определим оператор
определим оператор![]() ,
который сеточной функции
,
который сеточной функции![]() с координатами
с координатами![]() сопоставляет сеточную функцию
сопоставляет сеточную функцию![]() с координатами
с координатами![]() ,
где
,
где![]() определяется левыми частями уравнений
(4). То есть
определяется левыми частями уравнений
(4). То есть

![]()
Таким образом, краевая задача (1), (2) аппроксимируется операторным уравнением
![]() ,
(5)
,
(5)
где
![]() – сеточная функция,
– сеточная функция,![]() .
Заметим, что оператор
.
Заметим, что оператор![]() симметрический и однородное уравнение
симметрический и однородное уравнение
![]() (6)
(6)
имеет нетривиальные
решения
![]() на сетке
на сетке![]() ,
кроме того, любое решение (6) есть
,
кроме того, любое решение (6) есть![]() на
на![]() .
Обозначим
.
Обозначим![]() подпространство сеточных функций из
подпространство сеточных функций из![]() ,
ортогональных
,
ортогональных![]() (например ортогональных к
(например ортогональных к![]() на
на![]() ).
Такую функцию будем обозначать
).
Такую функцию будем обозначать![]() .
.![]() принадлежит
принадлежит![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
Заметим, что
![]() принадлежит
принадлежит![]() при любом
при любом![]() из
из![]() .
Действительно, поскольку
.
Действительно, поскольку![]() ,
то
,
то
![]() .
.
Отсюда следует,
что уравнение (5) имеет решение тогда и
только тогда, когда
![]() принадлежит
принадлежит![]() и любое решение определено с точностью
до
и любое решение определено с точностью
до![]() на
на![]() .
.
Условимся выбирать
решение уравнения (5) принадлежащее
![]() .
Если
.
Если![]() какое-то решение (5), то
какое-то решение (5), то![]() принадлежит
принадлежит![]() ,
где
,
где
 ,
,
а
![]() – сеточная функция, равная
– сеточная функция, равная![]() на всех точках сетки. Действительно
на всех точках сетки. Действительно![]() ,
поэтому
,
поэтому
 .
.
Уравнение
(5) на подпространстве
![]() невырожденное и
невырожденное и
![]() ,
,
где
![]() – наибольшее собственное значение
оператора
– наибольшее собственное значение
оператора![]() ,
,![]() – наименьшее неравное нулю собственное
значение. Если для решения уравнения
(5) мы воспользуемся итерационным
процессом, то нужно следить, чтобы
итерации не выходили из
– наименьшее неравное нулю собственное
значение. Если для решения уравнения
(5) мы воспользуемся итерационным
процессом, то нужно следить, чтобы
итерации не выходили из![]() .
Этого легко добиться при использовании
явного итерационного процесса
.
Этого легко добиться при использовании
явного итерационного процесса

В этом случае
![]() (7)
(7)
Откуда следует,
что если
![]() .
.
Заметим здесь,
что если для решения задачи (5) потребуется
большое число итераций, то, в силу
накопления погрешностей
![]() может выходить из
может выходить из![]() ,
поэтому следует через некоторое
количество итераций подправлять
,
поэтому следует через некоторое
количество итераций подправлять![]() ,
то есть заменять
,
то есть заменять![]() на
на
 .
(8)
.
(8)
