4. 8. Расчет на потерю напряжения разомкнутых электросетей

Расчет сети на потерю напряжения сводится к определению сечений участков S_k при заданных токах нагрузки l_k н, длинах участков l_k и конфигурации сети, при которых потеря напряжения в сети ∆U не превышает допустимого значения ∆U _доп ∆U < ∆U _доп.

В любой разомкнутой сети по известным токам нагрузок I _kH просто определяются токи на участках линии l_k, значение которых не­обходимо для определения сечений участков S_k.

Разомкнутые сети для расчета на потерю напряжения могут быть сведены к нескольким типам, представленным на рис. 4. 5.

Рис. 4.5. Типовые расчетные схемы разомкнутых сетей:

а – с одной сосредоточенной нагрузкой; б – с равномерно распределенной нагрузкой; в – с несколькими сосредоточенными нагрузками;

г – с разветвленной на конце; д – произвольно разветвленная

1. Простая разомкнутая сеть с одной сосредоточенной нагрузкой

Потеря напряжения в линии (рис. 4. 6) складывается из падения напряжения в проводе ∆U _пр = Ir = Il/γS и падения напряжения в переходных контактах ∆U _пр = IΣr_пер .

∆U = ∆U _пр+∆U _пер = Il/γS + IΣr_пер.

Из уравнений сечение провода определяется

S = Il/γ(∆U _доп - IΣr_пер).

Если пренебречь потерей напряжения в переходных контактах или в случае сплошного провода, то получим

S = Il/γ∆U_доп.

Отсюда можно найти так называемую критическую длину провода l_кр, для   которой  каждому выбранному по таблице сечению S = S_таб соответствует допустимый по нагреву ток I = I_доп 

Lкр = γS_таб∆U_доп /I _доп.

Рис. 4.6. Простая разомкнутая сеть с одной сосредоточенной нагрузкой.

U_A – напряжение источника; U_B – напряжение нагрузки; ∆U_пр – потеря напряжений в приводе; I_н – ток нагрузки; I – ток в линии;

1, 2, 3 – переходные контакты

Если фактическая длина линии не более критической (l < l_кр) для заданного ∆U_доп, то потерю напряжения в линии можно не опреде­лять, так как ∆U < ∆U_доп

Из анализа уравнения вытекает, что решение поставленной задачи имеет смысл только при ∆U > ∆U_доп;

Если задана относительная потеря напряжения

∆U % = (∆U /U_ном)100 %

при условии, что ∆U %< 100 %, то уравнение запишется

S = 100Il / γU_ном∆U %.

Если задана потеря мощности

∆Р % = (∆P /P_ном)100 % = (I2r/U_номI) 100 %,

то из уравнения получаем известную формулу Доливо-Добровольского:

S = 100 P_ном l/γU²_ном P_ном %.

2. Простая разомкнутая сеть с равномерно распределенной

нагрузкой

Пусть нагрузка равномерно распределяется на части линии. На рис. 4. 7 показаны такая линия, график распределения тока I_н и потери напряжения ∆U вдоль линии.

Потеря напряжения в линии складывается из двух составляющих

∆U_a2 = ∆U_a1 + ∆U₁₂

Очевидно, при постоянном сечении линии S = const потеря напряжения на участке a1 равна

∆U_a1 = I_Hr_a1 = I_HL₁/γS.

Потеря напряжения ца участке 1 – 2 с распределенной нагрузкой находится так:

.

Рис. 4.7. Простая разомкнутая сеть с равномерно распределенной нагрузкой.

I_н- суммарный ток нагрузки; I_L- ток в сечении L; ∆U_А2- потеря напряжения в сети; ∆U_А1, ∆U_АL, ∆U₁₂- потеря напряжения на соответствующих участках сети.

Из уравнений находим сечение провода

S = I_Hl_пр/γ∆U_доп .

Приведенная длина линии l_пр при равномерной нагрузке:

l_пр= L_{1 +} (L₂ - L₁)/2.

Таким образом, линия с равномерно распределенной суммарной нагрузкой I_H эквивалентна линии с сосредоточенной нагрузкой I_H, приложенной к середине загруженного участка линии. Если нагрузка равномерно распределена вдоль всей линии (l₁ = o), то приведенная длина определяется как l_пр=0,5L₂; если при этом налицо некоторая не­равномерность распределения нагрузки, то l_пр = (0,4 ÷ 0,6) L₂, причем 0,4 соответствует большей нагрузке в конце линии, а 0,6 – в начале линии.

3. Разомкнутая сеть с несколькими сосредоточенными нагрузками (рис. 4.8).

Рис. 4.8. Разомкнутая цепь с несколькими сосредоточенными нагрузками:

∆U- потеря напряжения в сети; ∆U₁, ∆U₂… ∆U _k- потеря напряжения на участках; I₁,I₂…I_k- токи на участках; r₁(l₁), r₂(l₂)…r_k(l_k)- сопротивления(длины) участков; R₁(L₁), R₂(L₂)… R_k(L_k)- сопротивления(длины) частей линии от источника А до приложения соответствующего тока нагрузки; I_1н, I_2н… I_kн- токи нагрузок

,

где I_k – сила токов,

R_k – сопротивление,

L_k – длина,

ΔU_k – падение напряжения,

I_kn – токи нагрузки потребителей,

R_ka – сопротивления участков сети,

L_ka – длины от питательного  пункта А до точки приложения k - ой нагрузки.Потери напряжения в сети

(4. 12)

при n сосредоточенных нагрузках

от А до К нагрузки (4. 13)

Из (4. 12) и (4. 13) уравнение потери напряжения в сети с n неизвестными сечениями участков Sк

(4. 14)

Дополнительные условия S_k = const, j_k = const, вес сети V = V_min

Первый вид расчета: S = Sk = const

Выражение (4. 14) можно записать в двух видах:

(4. 15)

(4. 16)

Введем понятие – суммарный момент токов относительно пункта А из (4. 15) и (4. 16)

(4. 17)

Искомое сечение сети S = M/γU_доп

Удельное сопротивление меди при температуре То = 15 ^оС –

0.0175, Ом мм² /м; при температуре Т –

Второй вид расчета: –const.

Запишем (4. 14) в виде:

. (4. 18)

Из (4.18) j_расч = γΔU_доп/L,

где L – длина линии с допустимой потерей напряжения

ΔU_доп.– допустимые потери напряжения в линии.

Тогда S_k = I_k / j_расч .

Третий вид расчета: расчет на минимум веса сети. V = V_min

(4. 19)

(4. 20)

S_k = I_kl_k/γ ΔU_k

из (4. 19) и (4. 20) имеем

(4. 21)

Найдем минимум функции U = U(ΔU₁ ΔU_2... ΔU_k…… ΔU_n-1).

Из уравнения (4. 21) получим

. (4. 22)

Из (4. 22) с учетом (4. 21) (4. 23)

и (4. 24)

Пример: Дана сеть с несколькими сосредоточенными нагрузками (рис. 4. 9). Рассчитать тремя методами объем проводов.

На 4. 9 введены обозначения: v_S – объем меди сети при расчете на постоянство сечения; v_j – объем меди при расчете на постоянство плотности тока; v_min – минимум меди сети при заданной потере напряжения; S₁, S₂-– сечения участков сети.

1. S₁ = S₂ = S S₁/S₂ = 1

Рис. 4.9. График сравнения трех видов расчета сети с несколькими сосредоточенными нагрузками

2. (4. 25)

3)

При любом способе расчета данной сети наиболее нагруженным в тепловом отношении является головной участок, который в первую очередь проверяется по допустимому нагреву. Нетрудно показать, что наиболее рациональное распределение меди между участками с точки зрения нагрева получается при расчете на постоянство плотности тока.

В общем случае расчет разомкнутой сети с несколькими сосредоточен­ными нагрузками надо вести всеми тремя способами, выбирая каждый раз ближайшие стандартные сечения участков (для головного участка и рядом лежащих – ближайшие большие, для концевых – ближайшие меньшие).

После этого надо проверить реальную потерю напряжения и нагрева, затем путем сравнения трех фактических вариантов расчета выбрать оптимальный.

4. Разомкнутая, произвольно разветвленная сеть

Исходными данными для расчета, как и во всех предыдущих сетях, являются токи нагрузок I_kH, длины участков l_k и допустимые потери напряжений от источника до всех потребителей. Расчет таких сетей хотя и громоздок, но в конечном счете сводится к применению ранее изложенных методов расчета разомкнутых сетей.

На рисунке представлена разомкнутая, произвольно разветвленная сеть и последовательность ее расчета, которая сводится к следующему:

1. Выбирается одно из направлений за магистральное (например, ABCDEFG), сосредоточив все нагрузки в точках этой магистрали

Критерием для выбора магистрального направления может быть или максимально допустимая потеря напряжения или максимум суммы произведений токов на участках на длину участков () для выбранного направления.

Рис 4.10. Разомкнутая, произвольно разветвленная сеть.

а – исходная сеть, б – расчетная сеть по магистральному направлению, в – расчетные сети разветвлений

2. Полученная разомкнутая сеть с несколькими сосредоточенными нагрузками (см. рис) рассчитывается тремя методами (Sk = const, jk = const и V = V_mln) и выбираются оптимальные сечения участков магистрали S_AB, S_BС, S_CD, S_DE, S_EF и S_FG.

3. Подсчитывается потеря напряжения на участках магистрали от питательного пункта А до точек приложения сосредоточенных нагрузок ΔU_AB, ΔU_AС, ΔU_AD, ΔU_AE, ΔU_AF.

4. Определяется допустимая потеря напряжения на разветвлениях относительно выбранной магистрали

ΔU_DQ = ΔU_AQ(доп) - ΔU_{АD ,}

ΔU_BP = ΔU_AP(доп) - ΔU_АB ,

ΔU_BR = ΔU_AP(доп) - ΔU_АB.

5. Рассчитываются   сечения   участков разветвлений (рис. 4. 12) по законам расчета отдельных разомкнутых сетей с известными допустимыми потерями напряжений.

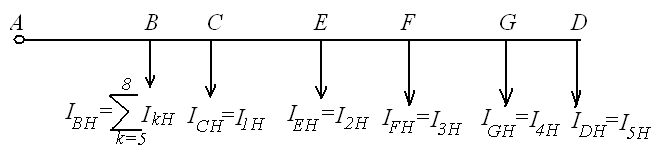
Рис 4. 11. К расчету сечений проводов

6. Проверяется, чтобы при выбранных сечениях Sk потери напряжения во всех направлениях исходной сети были не более допустимых значений.

В общем случае подобный расчет следует произвести для двух-трех магистральных направлений и затем выбрать оптимальный с точки зрения получения минимума веса и максимума эластично­сти сети.