
- •§ 2. Многочлены
- •1О. Эвристические соображения.
- •2O. Точные определения.
- •30. Деление многочленов.
- •4O. Делители многочленов. Наибольший общий делитель.
- •Определение 5. Многочлены называют взаимно простыми, если их общими делителями являются только многочлены нулевой степени.
- •Определение 6. Число называетсякорнем , если. Теорема 6 (теорема Безу). Пусть . Тогда.
§ 2. Многочлены
1О. Эвристические соображения.
В школьном курсе
многочленом (полиномом) от одной
переменной
![]() с
коэффициентами изR
называется выражение вида
с
коэффициентами изR
называется выражение вида
![]()
Здесь под
![]() понимается некоторый символ, который
может принимать любые значения изR.
понимается некоторый символ, который
может принимать любые значения изR.
В дальнейшем будем
рассматривать многочлены как формальные
выражения. Более того, для удобства
формальной записи алгебраических
операций многочлены желательно
рассматривать как сумму бесконечного
числа слагаемых вида
![]() с конечным числом отличных от нуля
слагаемых:
с конечным числом отличных от нуля
слагаемых:![]() Тогда формулы для суммы и произведения
многочленов примут вид:
Тогда формулы для суммы и произведения
многочленов примут вид:
![]() ;
;
![]() ,
,
где
![]() .
.
2O. Точные определения.
Определение 1.
Многочленом
одной переменной с
коэффициентами из множества комплексных
чисел С
называется бесконечная последовательность
![]() ,
в которой лишь конечное число элементов
не равно нулю.
,
в которой лишь конечное число элементов
не равно нулю.
Множество многочленов
с коэффициентами из С
обозначается
![]() .
Аналогично вводится множество
.
Аналогично вводится множество
![]() многочленов с коэффициентами из
многочленов с коэффициентами из![]() .
Далее утверждения формулируются для
многочленов из
.
Далее утверждения формулируются для
многочленов из![]() ,
и, если не оговорено специально, они
справедливы для многочленов из
,
и, если не оговорено специально, они
справедливы для многочленов из![]() .
.
Введем операции
сложения и умножения многочленов. Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
где
,
где
![]() .
.
Очевидно, что
![]() и
и![]() имеют лишь конечное число ненулевых
элементов, то есть являются многочленами.
При этом, если
имеют лишь конечное число ненулевых
элементов, то есть являются многочленами.
При этом, если![]() имеет
имеет![]() ,
а
,
а![]() ненулевых элементов, то
ненулевых элементов, то![]() – не более чем
– не более чем![]() ,
а
,
а![]() – не более чем
– не более чем![]() ненулевых элементов.
ненулевых элементов.
Теорема 1. Операции сложения и умножения многочленов удовлетворяют следующим свойствам:
ассоциативность сложения и умножения многочленов, т.е.
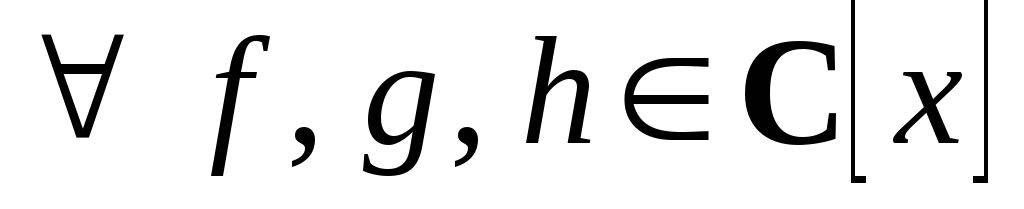 выполняются равенства
выполняются равенства ;
;коммутативность сложения и умножения многочленов, т.е.
 выполняются равенства
выполняются равенства ;
;дистрибутивность умножения относительно сложения, т.е.
 выполняется
выполняется ;
;для многочлена вида
 и
и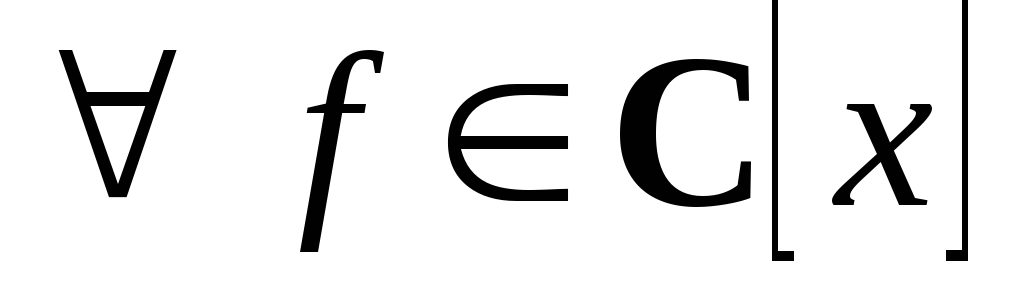 выполняется
выполняется ;
;для многочлена вида
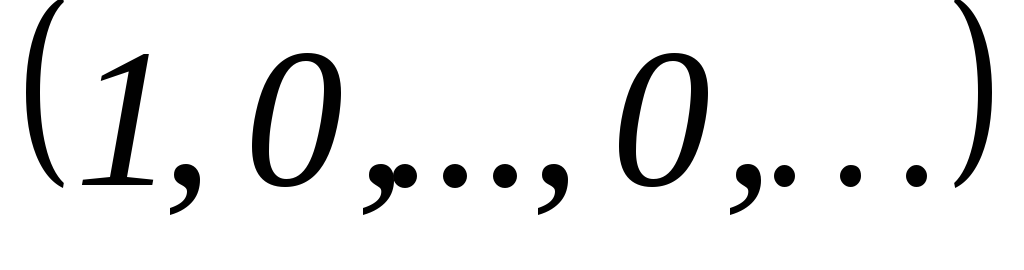 и
и выполняется
выполняется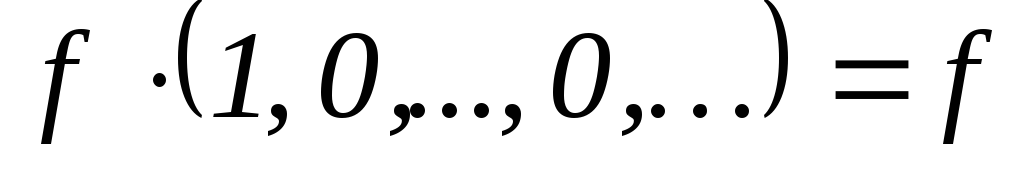 .
.
Доказательство. Проверим ассоциативность умножения. Пусть
![]() .
.
Необходимо доказать,
что
![]() .
Имеем:
.
Имеем:
![]() ,
где
,
где
![]() .
.
Тогда
![]() ,
,
где
![]() ,
,
и
![]() ,
где
,
где
![]() ,
,
то есть ассоциативность
умножения выполняется в силу ассоциативности
умножения в
![]() .
.
Проверим дистрибутивность, то есть выполнение равенства
![]() .
.
Имеем![]() где
где![]() ;
;
![]() где
где
![]() .
.
Проверим коммутативность умножения. Имеем
![]() ,
где
,
где
![]() и
и
![]() ,
где
,
где
![]()
![]() в силу коммутативности
умножения в С.
в силу коммутативности
умножения в С.
Аналогично проверяются остальные свойства. ■
Рассмотрим
![]() .
Очевидно, что
.
Очевидно, что
![]()
![]() .
.
Следовательно,
множество С'
можно отождествить с С
(то есть построить взаимно однозначное
соответствие между этими множествами,
так что
![]() ставится в соответствие
ставится в соответствие![]() .)
.)
Обозначим
![]() (так как
(так как![]() ).
).
Утверждение 1.
Пусть
![]() .
Тогда
.
Тогда![]() .
.
Доказательство.
Так как
![]() ,
то легко видеть, что
,
то легко видеть, что![]() .
Тогда
.
Тогда
![]() ,
и, значит
,
и, значит
![]()
![]() ■
■
Терминология.
Пусть
![]() .
Тогда
.
Тогда
![]() называется свободным
членом
многочлена. Если
называется свободным
членом
многочлена. Если
![]() ,
то
,
то
![]() называется степенью
многочлена.
Пишут
называется степенью
многочлена.
Пишут
![]() (degree),
(degree),
![]() – старший коэффициент
– старший коэффициент
![]() ,
,
![]() ,
,
![]() – переменная.
– переменная.
Следствие.
![]() выполняется
выполняется![]() .
.
При этом
![]() ,
,
![]() .
.
Доказательство.
Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
и![]() .
.
Если![]() или
или![]() .■
.■
Замечание.
![]() определено только для многочленов
нулевой степени
определено только для многочленов
нулевой степени![]() близко по свойствам к множеству целых
чисел
близко по свойствам к множеству целых
чисел![]() алгоритм деления с остатком.
алгоритм деления с остатком.
30. Деление многочленов.
Теорема 2.
Пусть
![]() .
Тогда
.
Тогда![]()
|
|
(1) |
Доказательство.
Пусть
![]() .
Если
.
Если![]() ,
то можно положить
,
то можно положить![]() .
Если
.
Если![]() ,
то будем использовать тот же метод
деления, что и для чисел. Пусть
,
то будем использовать тот же метод
деления, что и для чисел. Пусть
![]() и
и
![]() .
.
Положим
![]() .
Тогда
.
Тогда![]() .
Пусть
.
Пусть
![]() и
и
![]() .
Если
.
Если
![]() ,
то остановим процесс вычисления; если
,
то остановим процесс вычисления; если![]() ,
то положим
,
то положим![]() .
Пусть
.
Пусть![]() ,
,![]() – старший коэффициент
– старший коэффициент![]() ,
и так далее… Так как степени многочленов
,
и так далее… Так как степени многочленов![]() убывают, то получим
убывают, то получим![]() :
: и
и![]() .
Процесс останавливается. Суммируя
полученные ранее выражения, получаем:
.
Процесс останавливается. Суммируя
полученные ранее выражения, получаем:
 .
.
Тогда
 ,
,
![]() ,
то есть получено требуемое представление
(1).
,
то есть получено требуемое представление
(1).
Докажем единственность.
![]() Пусть
Пусть![]() и
и![]() .
Тогда
.
Тогда![]() .
Если
.
Если![]() ,
то
,
то![]() (по
лемме 1)
(по
лемме 1)![]() ,a
,a
![]() противоречие
противоречие![]() .■
.■
Определение 2.
Если
![]() и
и![]() ,
то
,
то![]() называетсяостатком
при делении
называетсяостатком
при делении
![]() на
на![]() .
.
Пример.
![]() .
Здесь
.
Здесь![]() .
.
Замечание.
Из указанного в теореме 2 алгоритма
деления с остатком следует, что если
![]() и
и![]() – многочлены с действительными
коэффициентами, то коэффициенты всех
многочленов
– многочлены с действительными
коэффициентами, то коэффициенты всех
многочленов![]() а значит и коэффициенты
а значит и коэффициенты![]() и
и![]() – действительные. Для целых коэффициентов
это утверждение неверно.
– действительные. Для целых коэффициентов
это утверждение неверно.
