РГР Нач геом / РГР 2_2 Взаимное пересечение тел

28

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Филиал государственного образовательного учреждения

высшего профессионального образования

«Уфимский государственный нефтяной

технический университет»

Филиал УГНТУ в г. Салавате

Кафедра «Оборудование предприятий нефтехимии и нефтепереработки»

Учебно-методическое пособие

к выполнению расчетно-проектировочной работы «Взаимное пересечение тел»

для студентов специальности 240801.65

очной и очно-заочной форм обучения

Уфа 2010

Пособие предназначено для самостоятельной работы студентов при выполнении расчетно-графической работы «Взаимное пересечение тел». Пособие содержит варианты заданий и примеры выполнения задачи. Рекомендуется для студентов очной и заочной форм обучения при изучении дисциплины «Начертательная геометрия. Инженерная графика»

Составитель Алушкина Т.В., доц. канд. техн. наук

Рецензенты:

© Уфимский государственный нефтяной технический университет, 2010

Расчетно-графическая работа № 2

Часть 2. Взаимное пересечение тел

Цель работы:

Освоить основные приемы построения линии пересечения геометрических тел. Изучить метод вспомогательных плоскостей и метод сфер. Научиться пользоваться ими при решении комплексных задач.

Для выполнения работы необходимо знать основные положения начертательной геометрии:

-понятия кривой линии;

-понятия опорных точек;

-сущность способа вспомогательных плоскостей;

-сущность метода концентрических сфер и область его применения;

- сущность метода эксцентрических сфер и область его применения.

Работа состоит из двух задач, при решении которых необходимо уметь:

-пользоваться указанными методами;

-уметь находить опорные точки, точки видимости;

-находить проекции точек принадлежащих поверхности.

Работа выполняется на формате А2. Исходные данные, рамка, штамп выполнить простым карандашом в соответствии с ГОСТами ЕСКД. Дополнительные построения выполнять цветными карандашами или пастой (синей, зеленой и т.д.), конечный результат построений выделить красным цветом.

Все надписи на чертеже выполняются простым карандашом шрифтом №5, индексы – шрифт №3,5.

Исходные данные к задаче 1 представлены в Приложении А, к задаче 2 – в Приложении Б.

Метод вспомогательных секущих плоскостей

Метод используется для определения проекций линий пересечения двух геометрических тел: многогранника и поверхности вращения, двух многогранников, двух поверхностей вращения.

При решении задач на взаимное пересечение поверхностей следует помнить следующие положения:

1. Чтобы найти точку, принадлежащую линии пересечения необходимо оба геометрических тела рассечь вспомогательной плоскостью так, чтобы в сечении плоскостью образовались простые фигуры – отрезок, окружность, треугольник, прямоугольник. Рассматривается пересечение простых фигур и определяются общие точки. Использование нескольких вспомогательных плоскостей позволяет определить ряд точек линии пересечения. Соединять можно только те точки, которые находятся на одной грани многогранника.

2. Если боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения уже есть и она совпадает с проекцией поверхности.

3. Если линия, принадлежащая поверхности, видна не полностью, то точки перехода от видимой части линии пересечения к невидимой располагаются на очерке геометрического тела. Видимая часть линии пересечения должна быть видимой одновременно для двух геометрических тел.

4. Чтобы найти верхнюю или нижнюю точку линии пересечения (конуса и многогранника), соответствующей грани с конусом, нужно взять плоскость, которая должна проходить через вершину конуса перпендикулярно грани многогранника (ребрам многогранника).

5. Чтобы найти верхнюю или нижнюю точку линии пересечения (сфера и цилиндр), необходимо провести вспомогательную плоскость через оси двух поверхностей.

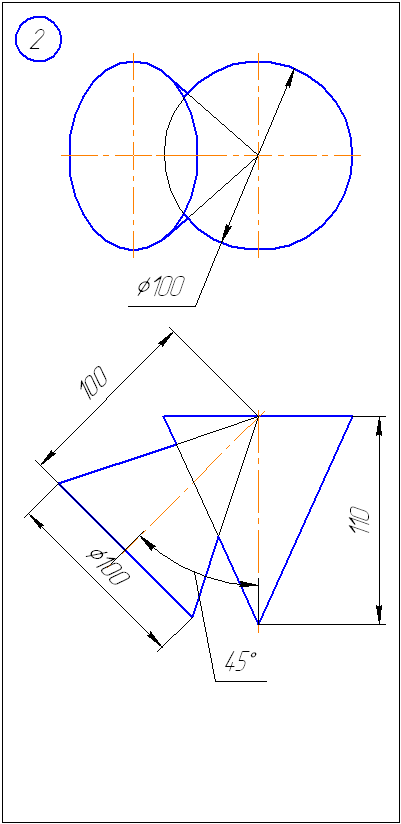
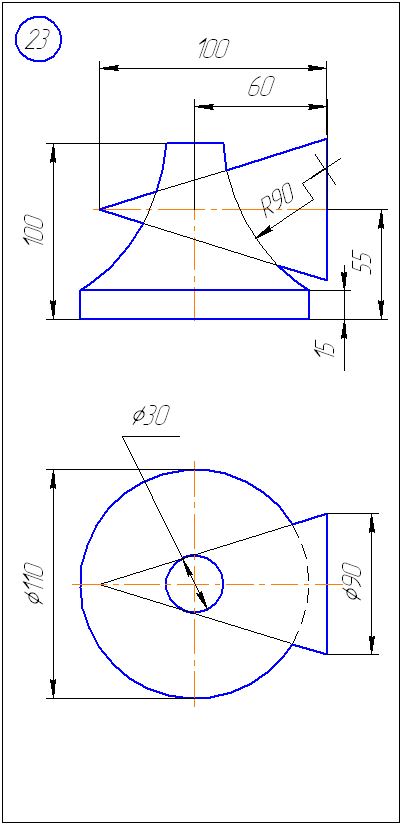
Условие задачи 1:

Построить проекции линии пересечения двух геометрических тел. При решении задачи использовать метод вспомогательных секущих плоскостей.

Рисунок 1

Алгоритм решения задачи:

1 В данной задаче образующие (ребра) призмы расположены перпендикулярно плоскости проекций П₂, следовательно, одна готовая проекция линии пересечения уже есть – на плоскости П₂.

При решении задачи в первую очередь необходимо найти опорные точки – это высшая и низшая точки, либо точки, которые можно определить без дополнительных построений. Находим высшую точку 1.

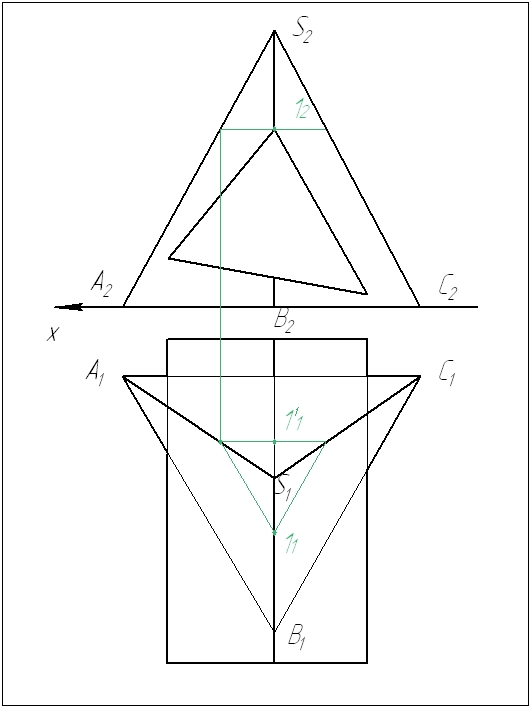
Определяем остальные опорные точки – 2 и 3.

2 Между опорными точками проводим вспомогательную секущую плоскость так, чтобы в сечении образовались простые фигуры: треугольник (для пирамиды) и прямоугольник (для призмы). Пересечение этих фигур дает нам искомые точки 4 и 5.

3 В случае, если находится линия пересечения поверхностей вращения необходимо проводить несколько вспомогательных плоскостей. Для определения линии пересечения гранных поверхностей достаточно найти точки пересечения граней с ребрами и получим проекции ломанной линии пересечения.

4 Соединяем точки в последовательности, определенной на фронтальной плоскости проекций. Определяем видимость полученной линии пересечения.

Метод сфер

Существуют две разновидности метода сфер:

- метод концентрических сфер;

-метод эксцентрических сфер.

Для каждого из этих методов существует ряд ограничений по области применения. Метод сфер применим, если:

- оба геометрических тела являются поверхностями вращения;

- оси поверхностей лежат в плоскости, параллельной плоскости проекций.

Сущность метода сфер заключается в следующем:

На пересечении осей поверхностей берется центр сфер. Проводится сфера произвольного радиуса. Сфера пересекает поверхности по окружностям, которые на эпюре вырождаются в отрезки. Рассматриваем пересечение отрезков, ищем общие точки. Найденные точки будут принадлежать искомой линии пересечения поверхностей. Проводим следующую вспомогательную сферу, построения повторяем, и т.д. Найденные точки соединяем плавной кривой.

Рассмотрим варианты пересечения поверхностей.

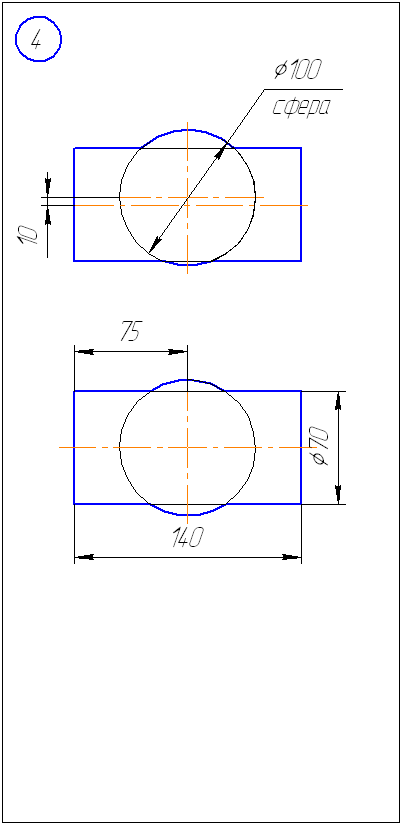
Задача 1. Построить линию пересечения двух поверхностей, одна из которых – сфера. Определить видимость. Задачу решить методом концентрических сфер.

Рисунок

Решение:

Данную задачу можно отнести к частному случаю. Таким способом можно решать задачу только в случае, если одно из тел – сфера.

1. Определяем опорные точки: высшую 1 и низшую 2. Находим их проекции.

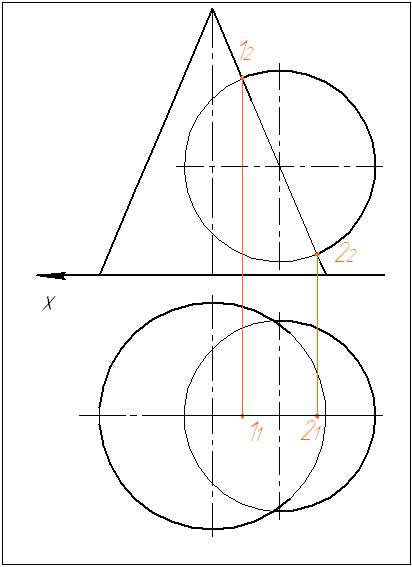
2. На оси конуса произвольно выбираем точку О₂ – центр сфер. Определяем величину минимально допустимого радиуса сферы:

.

Определяем максимально допустимый радиус сферы:

.

Диапазон значений радиусов сфер:

.

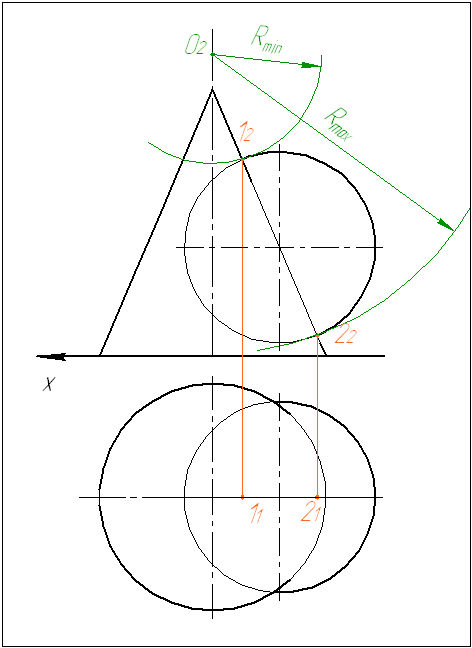
3. Проводим вспомогательную сферу. Определяем пересечение сферы с поверхностями как точки пересечения очерков поверхностей с дугой. Проводим отрезки и определяем их точку пересечения.

4. Проводим следующую сферу. Построения повторяем.

5. Соединяем полученные точки плавной кривой.

6. Достраиваем горизонтальную проекцию линии пересечения. Для этого рассматриваем найденные точки как точки, принадлежащие поверхности конуса. Полученные точки соединяем плавной кривой с учетом видимости.

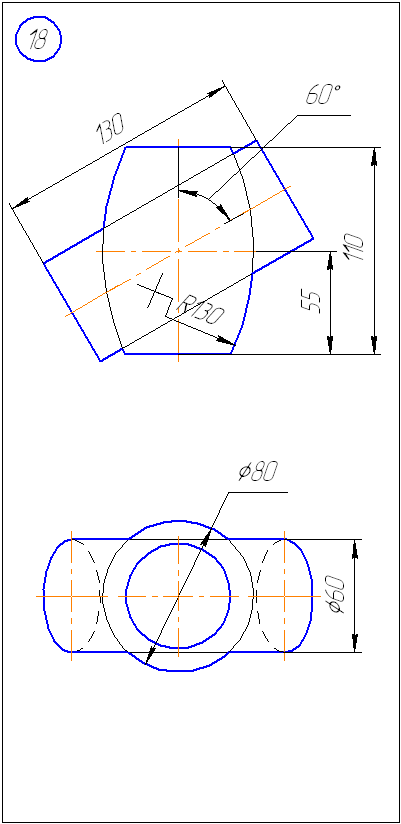
Задача 2. Построить проекции линии пересечения поверхностей. Определить видимость. Задачу решить методом концентрических сфер.

Рисунок

Решение:

1. Определяем опорные точки, как точки пересечения очерков поверхностей.

2. Определяем центр сфер – как точку пересечения осей.

3. Определяем максимально возможный радиус сферы

4. Определяем минимально возможный радиус сферы. Для этого из центра сферы проводим перпендикуляры к образующим поверхностей.

5. Вписываем сферу минимального радиуса. Сфера касается поверхности конуса по окружности и пересекает поверхность цилиндра по окружности. Обе этих окружности на эпюре вырождаются в отрезки. Рассматриваем пересечение отрезков, ищем общие точки.

6. Вписываем сферу произвольного радиуса R. Построения повторяем.

7. Количество вписанных сфер должно быть не менее трех. Полученные таким образом точки, соединяем плавной кривой.

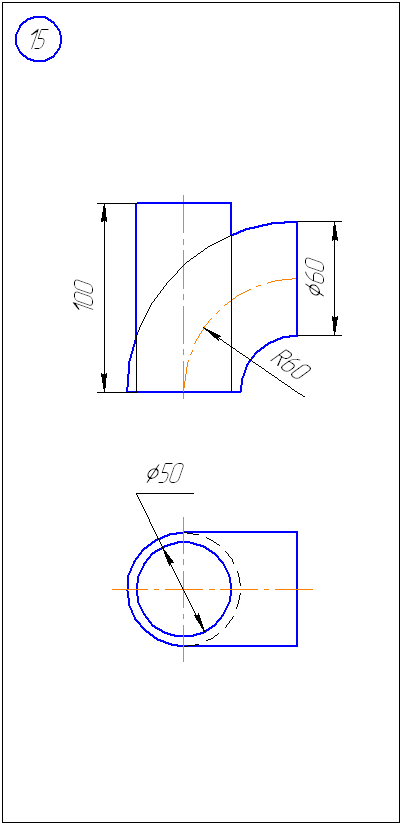
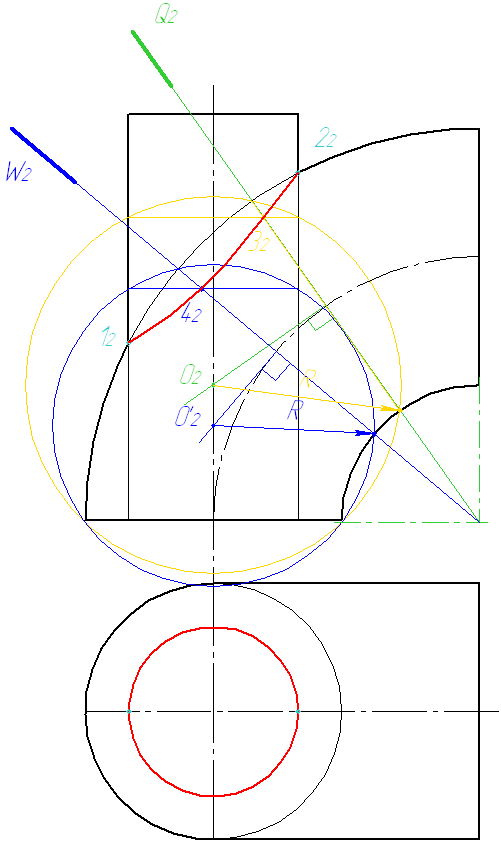
Задача 3. Построить проекции линии пересечения тора с цилиндром. Определить видимость. Задачу решить методом эксцентрических сфер.

Рисунок

Метод эксцентрических сфер применим, если:

- оба геометрических тела поверхности вращения;

- оси поверхностей лежат в плоскости, параллельной плоскости проекций;

- одна из поверхностей – тор.

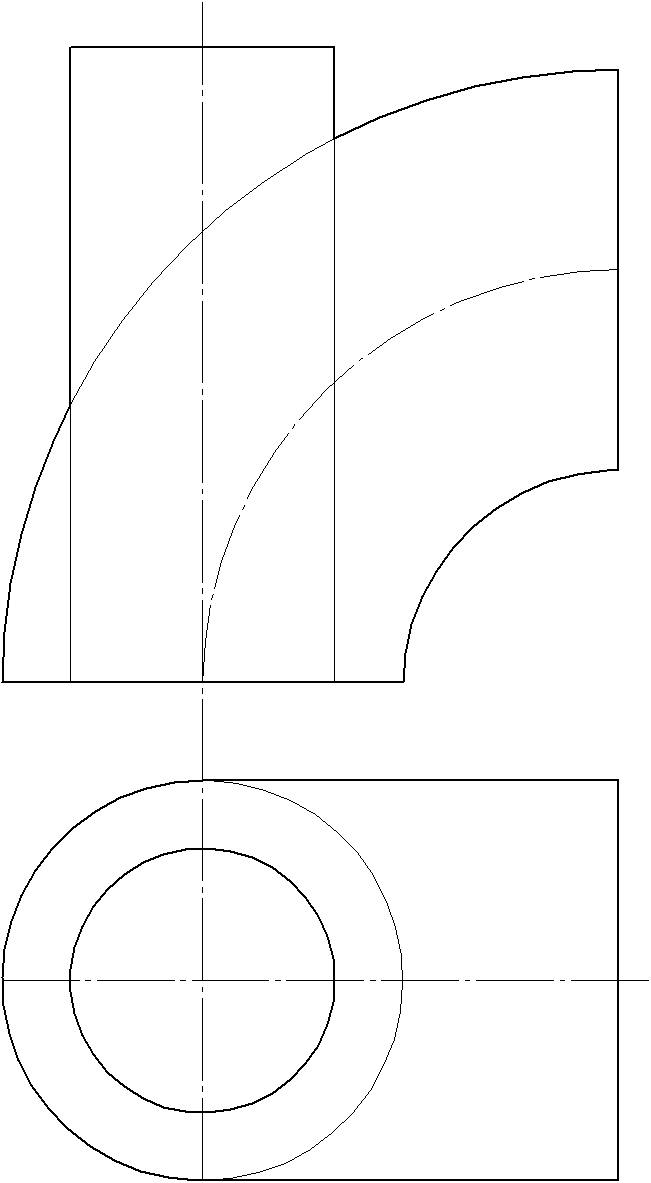
Решение:

1. Определяем опорные точки как точки пересечения очерков.

2. Проводим проецирующую плоскость в интервале между опорными точками. Из точки пересечения проецирующей плоскости с осью тора восстанавливаем перпендикуляр до пересечения осью цилиндра. Получим точку О – центр сфер.

3 Из центра О₂ проводим сферу радиуса R. Сфера будет пересекать поверхности цилиндра и тора по окружностям, которые на эпюре вырождаются в отрезки. Искомая точка лежит на пересечении полученных отрезков.

4. Проводим следующую проецирующую плоскость. Построения повторяем.

5 Количество сфер выбирается самостоятельно, но не менее трех.

Соединяем полученные точки плавной кривой. Находим вторую проекцию линии пересечения.

Приложение А – Варианты заданий к задаче 1 (метод секущих плоскостей)

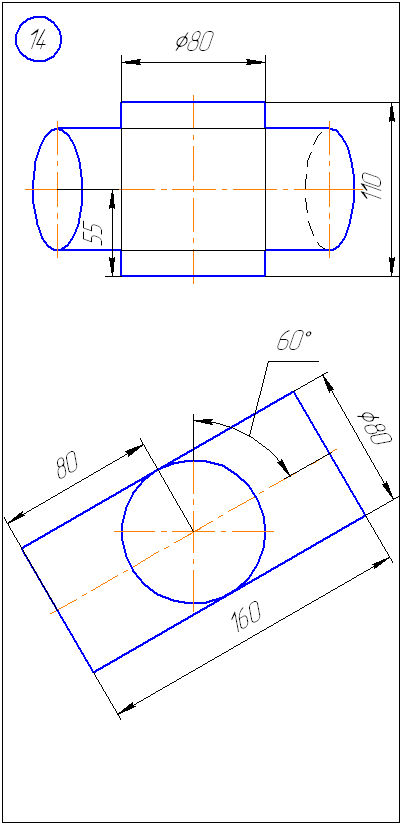
Приложение Б – Варианты заданий к задаче 2 (метод сфер)