
2. Представление сигналов / Лабораторная 2. Представление сигналов. Агеев
.docxМИНОБРНАУКИ
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«Челябинский государственный университет»
(ФГБОУ ВО «ЧелГУ»)
Кафедра радиофизики и электроники
Лабораторная работа №2
«Представление сигналов»
-
Выполнил:
студент группы ФФ-404
Агеев Алексей
Проверил:
Доцент, Старший научный сотрудник
Павлухина О.О.
Челябинск, 2025 г.
Задание:
Отрисовать Гауссову кривую,
 ,
с параметрами:
,
с параметрами:

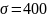
Получить данные
Представить произвольный сигнал в виде суммы функций Хевисаида.
Формула, описывающая график:

Ход работы:
Пишем программу в C++:
#include <iostream>
#include <fstream>
#include <cmath>
using namespace std;
const double pi = 3.141592653589793;
double heviside(double n)
{
if (n < 0) return 0.0;
else return 1.0;
}
double gaus(double n, double M, double G)
{
return 10000000 * exp(-pow(n - M, 2) / (2 * G * G)) / (G * sqrt(2 * pi));
}
void gen_graf_gaus(double M, double G)
{
ofstream out;
out.open("gaus.dat");
for (int n = 0; n < 1000; n++)
{
out << n << " " << gaus(n, M, G) << "\n";
}
out.close();
}
void gen_graf_heviside(double A, double k)
{
ofstream out;
out.open("heviside.dat");
for (int n = -100; n < 100; n++)
{
out << n << " " << A * heviside(n - k) << "\n";
}
out.close();
}
int main()
{
double G = 400.0, M = 500.0;
int N = 1000;
double* f_gaus = new double[N];
ofstream out;
out.open("gaus.dat");
for (int n = 0; n < N; n++)
{
f_gaus[n] = gaus(n, M, G);
out << n << " " << f_gaus[n] << "\n";
}
out.close();
int K;
cout << "Enter number of steps (K): ";
cin >> K;
int dn = N / K;
int dn = N / K;
double* s = new double[N];
for (int n = 0; n < N; n++)
{
s[n] = 0.0;
}
for (int n = 0; n < N; n++)
{
s[n] = f_gaus[0] * heviside(n);
for (int k = 1; k < K; k++)
{
double delta = f_gaus[k * dn] - f_gaus[(k - 1) * dn];
s[n] += delta * heviside(n - k * dn);
}
}
out.open("approximation.dat");
for (int n = 0; n < N; n++)
{
out << n << " " << s[n] << "\n";
}
out.close();
gen_graf_heviside(500000, 200);
delete[] f_gaus;
delete[] s;
return 0;
}
При 10 (в коде меняем N на 100, мю на 50, сигма на 40):

При 1000:

