Васечкин Андрей ПТМ-014

1) Какие существуют способы задания движения точки?

1. Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

2. Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

2. Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

2) Как определяется скорость и ускорение точки при задании ее движения векторным способом?

При векторном способе задания движения положение точки на плоскости или в пространстве определяется вектором-функцией

r = r(t)

Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса- вектора и направлена по касательной к годографу r (по касательной к траектории движения точки)

5. = dr/dt

Ускорение точки (изменение ее скорости) определяется как производная от скорости:

Вектор ускорения направлен по касательной к годографу вектора скорости.

3) Что называется годографом вектора?

Годографом вектора являющегося функцией скаляра называется геометрическое место точек, которое описывает конец этого вектора при изменении скаляра когда начало вектора помещено в фиксированную точку О пространства.

4) Что такое траектория точки?

Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.

5) Как записываются уравнения движения точки в декартовых координатах?

Положение точки М в пространстве с использованием данной системы координат задается ее координатами x, y, z. Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде: x=x(t), y=y(t), z=z(t).

x=x(t), y=y(t), z=z(t) - представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме, где параметром является время t.

6) Как определяется скорость точки при задании ее движения координатным способом?

Из определения скорости:

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями:

7) Как определяется ускорение точки при задании ее движения координатным способом?

Из определения ускорения:

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени:

Модуль и направление ускорения определяются выражениями:

8) Что необходимо задать, чтобы определить движение точки естественным способом?

Для задания движения точки естественным способом надо задать:

1-траекторию;

2-начало отсчета дуговой координаты с указанием положительного и отрицательного направлений отсчета;

3-закон движения точки вдоль траектории S = S(t).

9) Как называются и как направлены оси подвижной системы координат, применяющейся при естественном способе задания движения точки?

При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

• τ — орт касательной;

• n — орт нормали;

• b — орт бинормали;

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

10) По какой формуле определяется скорость точки при естественном способе?

Модуль скорости, т.е. ее численное значение, при естественном способе задания движения

точки определятся так: .

11) Как направлен вектор скорости точки по отношению к ее траектории?

Вектор скорости направлен по касательной к траектории точки в сторону движения.

12) Как определяется ускорение точки при естественном способе задания ее движения?

Из определения ускорения точки

поскольку τ — переменный по направлению вектор, то:

Производная

определяется только свойствами траектории в окрестности данной точки, при этом

n — единичный вектор главной нормали, ρ — радиус кривизны траектории в данной точке.

Таким образом,

т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:

13) Что характеризует касательное ускорение точки и как оно направлено?

Касательное ускорение точки характеризует изменение вектора её скорости по величине. Вектор касательного ускорения направлен по касательной к траектории движущейся точки в ту же сторону, что и вектор скорости точки, когда движение точки ускоренное, и в обратную сторону, когда – замедленное.

14) Напишите формулу, по которой определяется касательное ускорение точки.

Касательное ускорение точки равно первой производной от модуля скорости или второй

производной от расстояния по времени. Касательное ускорение обозначается – .

15) В каких случаях касательное ускорение точки равно нулю?

Касательное ускорение равно нулю при движении точки с постоянной по модулю скоростью.

16) Что характеризует нормальное ускорение точки и как оно направлено?

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело.

17) Напишите формулу, по которой определяется нормальное ускорение точки. Числовое значение нормального ускорения определяется в общем случае по формуле an = v²/R,

где v – модуль скорости точки в данный момент;

R – радиус кривизны траектории в месте, где находится точка в данный момент.

18) В каких случаях нормальное ускорение точки равно нулю?

Если нормальное ускорение точки равно нулю, то точка движется прямолинейно.

19) Как определить, ускоренно или замедленно движется точка?

При равноускоренном движении ускорение имеет такое же направление, как и скорость, его проекция, если тело движется в сторону положительного направления оси положительна. При равнозамедленном движении ускорение направлено противоположно скорости, его проекция отрицательна. Во всех формулах при равнозамедленном движении перед ускорением ставится знак минус.

Например: v=v0 +a*t (для равноускоренного движения). v=v0 - a*t .( для равнозамедленного движения)

20) Напишите уравнение равномерного движения.

Движение точки называют равномерным, если модуль ее скорости не зависит от времени

( ). Длина пути , пройденного равномерно движущейся точкой, является линейной функцией времени:

где — начальный момент времени, – время.

21) Напишите уравнение равнопеременного движения.

Формула скорости равнопеременного движения в любой момент времени:

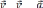
= 0 + t