2. Обоснование выбора типа идеального реактора

РИВ-Н представляет собой трубчатый аппарат, в котором отношение длины трубы к ее диаметру достаточно велико L/d > 20.

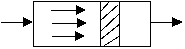
Рисунок 1 – Схема РИВ-Н

В реактор непрерывно подаются исходные реагенты, которые превращаются в продукты реакции по мере перемещения их по длине реактора. Любая частица потока движется прямолинейно и равномерно, не происходит ни продольного, ни поперечного перемешивания. Такой режим движения реагентов называется поршневым.

Концентрация исходного реагента А постепенно меняется по длине или высоте реактора от начального значения С_А0 до конечного значения С_А. Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же.

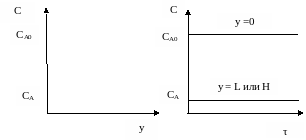
Рисунок 2 – Изменение концентрации реагента в реакторе

Исходным уравнением для вывода характеристического уравнения является материальный баланс в дифференциальной форме. Модель РИВ-Н предполагает движение реакционной смеси только в одном направлении – по х – координате, поэтому

где W – линейная скорость движения реакционной смеси, L – длина реактора.

В РИВ-Н отсутствует продольное и радиальное перемешивание, нет продольной и радиальной конвективной диффузии, а молекулярной диффузией можно пренебречь, поэтому .

После упрощения получаем характеристическое уравнение РИВ-Н в нестационарном режиме.

При стационарном режиме (нет накопления вещества).

Линейная скорость движения реакционной смеси в реакторе с постоянной площадью сечения в любой момент времени равна

, следовательно, .

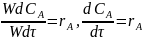
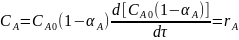
Разделим переменные и возьмем интегралы

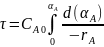- характеристическое уравнение РИВ-Н в стационарном режиме.

РИС-П представляет собой аппарат с мешалкой, в который непрерывно подают реагенты и также непрерывно выводят из него продукты.

Рисунок 3 – РИС-П с мешалкой

В таком реакторе создается интенсивное перемешивание, поэтому по всему реактора мгновенно устанавливается одинаковая концентрация реагента, равная концентрации на выходе. Резкое (скачкообразное) изменение концентрации происходит за счет мгновенного смешения поступающих реагентов с реакционной массой, уже находящейся в реакторе.

Рисунок 4 – Изменение концентрации реагента в реакторе

Величина перепада между начальной и конечной концентрацией зависит при прочих равных условиях от величины скорости химической реакции и от времени пребывания реакционной смеси в реакторе. Чем выше скорость и больше время, тем больше скачок концентрации.

Для РИС-Н характерно отсутствие градиентов параметров как во времени, так и по объему реактора, поэтому для вывода характеристического уравнения используют уравнение материального баланса в общей форме.

N_{А накопл.} = N_{А конвек.} - N_{А хим.р.}

При стационарном режиме N_{А накопл.} = 0.

N_{A конвек.} = N_{А приход} – N_{А сток}

N_{А приход} = N_А0 = C_А0 v_об., где v_об. – объемная скорость подачи реагента.

N_{А сток} = N_А0 (1-α_А) = C_А0 v_об. (1-α_А)

N_{A конвек.} = C_А0 v_об. - C_А0 v_об. (1-α_А) = C_А0 v_об.α_А.

N_{A хим.} =(-r_A) V_p, где V_p – объем реактора.

C_А0 v_об.α_А = =(-r_A) V_p, V_p = v_об τ

C_А0 v_об.α_А =(-r_A) v_об τ

C_А0α_А = (-r_A) τ

характеристическое уравнение для РИС-Н.

Для простой необратимой реакции «n»-го порядка

При n = 0 , при n = 1 .

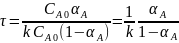Характеристические уравнения для РИС-П и РИВ-Н одинаковы, и время достижения заданной степени превращения реагента в этих реакторах одно и то же. Но в РИС-П полное время процесса складывается из рабочего времени, рассчитываемого по характеристическому уравнению, и вспомогательного времени на загрузку и выгрузку. В РИВ-Н вспомогательных операций нет, поэтому интенсивность РИВ-Н выше, чем в РИС-П.

В РИС-Н вспомогательных операций тоже нет, но гидродинамическая обстановка в нем отличается от обстановки в РИВ-Н, поэтому для достижения одной и той же степени превращения реагента при прочих равных условиях требуется большее время, чем в случае РИВ-Н.

Сравним концентрационные режимы в РИС-Н и РИВ-Н. В РИВ-Н наблюдается постепенное уменьшение концентрации реагента по длине реактора, а в РИС-Н – резкое падение концентрации до конечного значения.

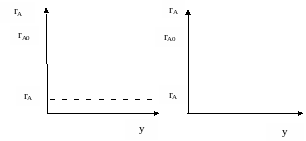
Рисунок 5 – Сравнение реакторов

Такой же характер для этих реакторов имеет изменение скорости реакции. Следовательно, средняя скорость реакции в РИС-Н всегда ниже, чем в РИВ.

Сравним характеристические уравнения реакторов в случае реакций разного порядка.

При n = 0 характеристическое уравнение РИС-Н и РИВ-Н имеет вид . Следовательно, время, необходимое для достижения заданной конверсии реагента одинаково; тип реактора в этом случае не оказывает влияния на интенсивность процесса. Это связано с тем, что при n = 0 скорость реакции не зависит от концентрации реагента.

При n > 0 тип реактора будет оказывать сильное влияние на интенсивность процесса.

> , т.е. .

Неравенство тем значительнее, чем больше конверсия реагента.

Рисунок 6 – Степень превращения

Для сложных процессов об эффективности судят не только по размерам реактора, но и по величине селективности. Для процессов, селективность которых зависит от концентрации реагента ( порядок целевой реакции ≠ порядку побочной реакции), на селективность можно повлиять, правильно выбрав тип реактора. Например, для сложно-параллельного процесса, в котором порядок целевой реакции выше порядка побочной реакции, для обеспечения высокой селективности необходимо поддерживать высокую концентрацию реагента. В этом случае лучше выбрать РИВ-Н. Если порядок целевой реакции меньше порядка побочной, нужно поддерживать низкую концентрацию реагента, поэтому более предпочтителен РИС-Н.

От типа реактора зависит и выход целевого продукта. Для сложно-параллельного необратимого процесса выход можно связать с селективностью следующими соотношениями:

РИС-Н β = S α_A; РИВ-Н .

При увеличении α_A

S уменьшается, если n_цел.р. > n_{побоч.р.}; S увеличивается, если n_цел.р. < n_{побоч.р.}.

β_РИВ-Н > β_РИС-Н β_РИС-Н > β_РИВ-Н

Рисунок 7 – Сравнение реакторов

Во время лабораторного синтеза борат 1-гидрокси-2,4-бисфениламиноантрахинона были получены следующие результаты, представленные в таблице 4. Начальная концентрация реагента равна 69 моль/л.

Таблица 4 – Зависимость концентрации реагента А от времени

№	Тип реакции	Тип реактора	Начальная концентрация, моль/л	Время реакции, мин
				1	2	3	4	5	15	30	45	60	90	115
10	A→ D A→C	РИС-П	69	68	67	67	66	66	62	52	45	35	24	9

Определяем порядок реакции графическим способом. В таблице 5 рассчитаны данные, необходимые для построения графиков для определения порядка реакции.

Таблица 5 – Данные для графического определения порядка реакции

t, мин	C, моль/л	lnC	1/C, л/моль	1/C2, л2/моль2
1	68	4,21950771	0,01470588	0,00021626
2	67	4,20469262	0,01492537	0,00022277
3	67	4,20469262	0,01492537	0,00022277
4	66	4,18965474	0,01515152	0,00022957
5	66	4,18965474	0,01515152	0,00022957
15	62	4,12713439	0,01612903	0,00026015
30	52	3,95124372	0,01923077	0,00036982
45	45	3,80666249	0,02222222	0,00049383
60	35	3,55534806	0,02857143	0,00081633
90	24	3,17805383	0,04166667	0,00173611
115	9	2,19722458	0,11111111	0,01234568

По данным таблицы 5 строим четыре графика, дающие возможность графически определить порядок реакции. Графики строим в координатах «t – C», «t – lnC», «t – 1/C», «t – 1/C²» так, чтобы на графике были видны расчетные точки, и соединяющая их линия была линейной линией тренда (рис. 8), выводим на график величину достоверной аппроксимации R².

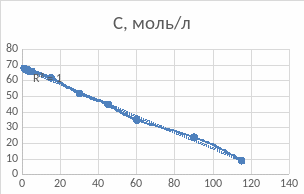
Рисунок 8 – Графический метод определения порядка реакции (а) - нулевой порядок, б) -первый порядок, в) -второй порядок, г) – третий порядок)

По представленной на каждом из графиков величине достоверности аппроксимации R² и характеру кривой, делаем вывод, что реакция 1-го порядка, так как в этом случае величина достоверности аппроксимации принимает наиболее близкое к единице значение, равное 0,9969.

Затем определяем порядок реакции аналитически. Для этого рассчитываем константы скорости k₀, k₁, k₂, k₃ для реакций 0-го, 1-го, 2-го и 3-го порядков в каждый момент времени по формулам соответственно:

,

,

,

,

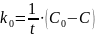где t – время контакта, мин;

С – концентрация исходного реагента в момент времени t, моль/л;

C₀ – начальная концентрация исходного реагента A, моль/л.

Результаты расчета заносим в таблицу 7.

Таблица 7 – Зависимость концентрации исходного реагента и константы скорости реакций различных порядков от времени

t, мин	C, моль/л			k0, моль/(л∙мин)		k1, (мин)-1		k2, л/(моль∙мин)		k3, л2/(моль2∙мин)
1		68		1		0,0145988		0,000213129		3,11153E-06
2		67		1		0,01470694		0,00021631		3,18171E-06
3		67		0,666666667		0,00980463		0,000144207		2,12114E-06
4		66		0,75		0,01111294		0,00016469		2,44106E-06
5		66		0,6		0,00889035		0,000131752		1,95285E-06
15		62		0,466666667		0,00713147		0,000109085		1,67019E-06
30		52		0,566666667		0,00942876		0,000157934		2,66304E-06
45		45		0,533333333		0,00949876		0,000171766		3,15319E-06
60		35		0,566666667		0,01131264		0,000234645		5,05239E-06
90		24		0,5		0,01173392		0,000301932		8,47817E-06
115		9		0,52173913		0,01771202		0,00084016		5,27636E-05
Показатель			k₀		k₁		k₂		k₃
Среднее арифметическое			0,65198		0,011448		0,00024415		0,000007872
Дисперсия			0,032527		0.0000087046		0.000000038204		0.00000000020488
СКО			0,18035		0,002950		0,00019546		0,000014314
Коэффициент вариации, %			21,66 %		25,77 %		80,06 %		181,84 %

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической, дисперсия дает характеристику разброса данных вокруг центра. То есть дисперсия — это математическое ожидание отклонений от математического ожидания. На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

,

где s²– выборочная дисперсия, рассчитанная по данным наблюдений,

X– отдельные значения,

X̅– среднее арифметическое по выборке,

n– количество значений в выборке.

Для расчета стандартного среднеквадратичного отклонения(СКО) необходимо из дисперсии извлечь квадратный корень. Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

,

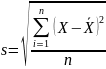Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность в разных выборках. Коэффициент вариации ‑ величина относительная, на его размер не оказывают влияние абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется в пределах от 0 до 100%, при этом значение коэффициента прямо пропорционально силе колеблемости. Коэффициент вариации рассчитывается по формуле:

,

Проведя анализ таблицы 7 можно сделать вывод, что, используя графический и аналитический метод, порядок реакции определен как первый и константа скорости реакции для дальнейших расчетов определена равной k₃=0,651 л²/(моль²∙мин).

Рисунок 9 – Зависимость концентрации реагентов от времени реакции.