ТОЭ3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

Отчет

по лабораторной работе № 3

Тема: «Исследование свободных процессов в электрических цепях»

Студент гр. 3206 _____________________ Корепанов Д. М.

Преподаватель _____________________ Константинова Е. В

Санкт-Петербург

2025

Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением её собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Схема установки

Схема установки исследования свободных процессов в электрических цепях представлена на рисунке 1.

Р ис. 1. Схема установки исследования свободных процессов в электрических цепях: а – первого порядка, б – второго порядка, в – третьего порядка.

Основные расчетные формулы.

1. Формула для расчета собственной частоты p₁ (Гц) у цепи первого порядка: p₁ = , где R – сопротивление резистора (Ом), C – емкость конденсатора (Ф).

Собственная частота p₁ по осциллограмме:

p₁= -α = , где α – постоянная затухания, для осциллограммы: α= , – постоянная времени. И U₁ – напряжение по осциллограмме в момент времени t₁, U₂ - напряжение по осциллограмме в момент времени t₂. Δt = t₂-t₁

2. Формула для расчета собственной частоты p_1,2 (Гц) у цепи второго порядка при колебательном процессе: p_1,2 = -α ± 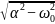*j, где

α = R₁/(2L), ₀ = 1/ . L – индуктивность катушки (Гн).

Частота ω = , где T – период.

Собственная частота p_1,2 по осциллограмме должная удовлетворять условию Δt=T!

3. Формула для расчета собственной частоты p_1,2 = p₁ = p₂ по осциллограмме для критического режима:

p_1,2=-α = , где

t_m – момент наступления максимума.

4. Формула для расчета экспериментальной добротности цепи второго порядка Q:

Q =

5. Формула для расчета теоретической добротности Q цепи второго порядка: Q=

Обработка результатов

1. Исследование свободных процессов в цепи первого порядка

Теоретическая собственная частота цепи:

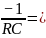
p₁ = = -10 000 с^-1 = -10⁴ с^-1

Рис.1 Диаграмма расположения собственной частоты цепи первого порядка.

Собственная частота цепи по осциллограмме:

График 1. Осциллограмма свободного процесса в цепи первого порядка

U₁ = [0,8 * 0,5] В; t₁ = [0,4 * 0,2] мс

U₂ = [0,2 * 0,5] В; t₂ = [1 * 0,2] мс

p₁= -α = = 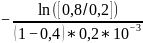≈ - 11552 с^-1.

2. Исследование свободных процессов в цепи второго порядка

Теоретическая собственная частота цепи при R₁ = 0,5 кОм (колебательный процесс):

p_1,2 = -α ± ;

α = R₁/(2L) = 0,5*10³/(2*25*10^-3)=10000.

= 1/LC=1/( =2 000 000 000 ≈

p_1,2 ≈ -10⁴ ± = -10⁴ ± j*4,36*10⁴ с^-1;

Рис. 2. Диаграмма расположения собственной частоты в цепи второго порядка. Колебательный режим

Собственная частота цепи по осциллограмме:

График 2. Осциллограмма колебательного процесса в цепи второго порядка

U₁ = [1.7 * 0.2] В; t₁ = [0,2 * 0,2] мс

U₂ = [0.3 * 0.2] В; t₂ = [0,6 * 0,2] мс

α = = 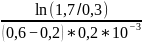≈21683 с^-1.

ω = 78539

p_1,2 ≈ -2,16*10⁴ ± 7,8*10⁴*j с^-1.

Q = 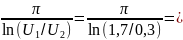1,81

3. Теоретическая собственная частота цепи при R₁ = 3 кОм (апериодический режим):

p_1,2 = -α ± ; α = R₁/(2L) = 3*10³/(2*25*10^-3)=60000.

= 1/LC=1/( =2 000 000 000 ≈

p_1,2 ≈ -(6*10⁴)±4,4*10⁴ с^-1.

Рис. 3. Диаграмма расположения собственной частоты в цепи второго порядка. Апериодический режим

Собственная частота цепи по осциллограмме:

График 3. Осциллограмма апериодического режима

U₁ = [1.2 * 0.2] В; t₁ = [0,4 * 0,2] мс

U₂ = [0.2 * 0.2] В; t₂ = [1 * 0,2] мс

p_1,2 ; α = = ≈ 14931 с^-1.

ω = 52360

p_1,2 =-α ± jω= -1,5*10⁴ ± 5,2*10⁴ с^-1.

4. Теоретическая собственная частота цепи при R₁=R_кр=2,24 кОм (установленный по осциллограмме критический режим):

p_1,2 = -α ± ;

α = R₁/(2L) =2,25 * 10³/(2*25*10^-3) = 45000

= 1/LC=1/( =2 000 000 000≈

p_1,2 ≈ -*10⁴ ± 4,5*10⁴ с^-1;

Для установки действительного критического режима правая часть выражения должна быть равна нулю, что возможно только при R₁≈2 236,0679 Ом. Найденный экспериментально критический режим отличается от теоретического на большую величину. На диаграмме будет представлено расположение собственной частоты при α = 2236,0679/(2*25*10^-3) ≈ 4,47*10⁴.

p_1,2 ≈ -4,47*10⁴

Рис. 4. Диаграмма расположения собственной частоты в цепи второго порядка. Критический режим

Собственная частота цепи по осциллограмме (t_m= [0,1*0,2]*10^-3с):

p_1,2 = = 50000 = 5 * 10⁴ с^-1.

График 4. Осциллограмма критического режима

Собственная частота цепи по осциллограмме различается от действительной теоретической на относительно малую величину, что говорит о неверных значениях сопротивления на переменном резисторе.

Добротность контура при R₁ = 0 Ом.

Q= = =0,6731…≈0,67

5. Теоретическая собственная частота цепи при R₁=R₄=0 кОм:

p_1,2 = -α ± ;

α = R₄/(2L) = 0

= 1/LC=1/( =2 000 000 000≈

p_1,2 ≈ ± 4,5*10⁴ с^-1;

Рис. 5. Диаграмма расположения собственной частоты в цепи второго порядка при R₁=R₄=0

График 5. Осциллограмма конденсатора при R = 0

U₁ = [0,8 * 0,5] В; t₁ = [0 * 0,1] мс

U₂ = [0,6 * 0,5] В; t₂ = [2,2 * 0,1] мс

α = = ≈ 13076 с^-1.

ω = 104720

p_1,2 =-α ± jω= -1,3*10⁴ ± 10,5*10⁴ с^-1.

6. Расчет теоретического значения собственной частоты контура для цепи третьего порядка:

Рис. 6. Диаграмма расположения собственной частоты в цепи третьего порядка.

Вывод

Проведена связь между видом свободного процесса в электрической цепи и расположением её собственных частот (корней характеристического уравнения) на комплексной плоскости. Составлены диаграммы расположения собственных частот цепи на комплексной плоскости, обработаны осциллограммы свободных процессов в цепях.

Большинство теоретических выкладок далеки от значений, найденных экспериментально. Так как в формулах расчёта теоретических значений переменными являются значения индуктивности, ёмкости и сопротивления исследуемых элементов, можно судить что различия в значениях собственной частоты вызваны отличием действительного значения характеристик этих элементов от используемых при экспериментальных исследованиях. Так как практически все исследуемые процессы соответствуют теоретическим, но расходится только по значениям частот.