9

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №9

Тема: ИССЛЕДОВАНИЕ ИНДУКТИВНО СВЯЗАННЫХ ЦЕПЕЙ

по дисциплине: Теоретические основы электротехники

Студент гр.3206		Корепанов Д. М.
Преподаватель		Константинова Е.В.

Санкт-Петербург

2025 г.

Цель работы: экспериментальное определение параметров двух индуктивно связанных катушек и проверка основных соотношений индуктивно связанных цепей при различных соединениях катушек.

Схема установки:

Рис.1. Схема для определения индуктивностей катушек, взаимной индуктивности и коэффициента связи

Рис.2. Последовательное соединение двух индуктивно связанных катушек

Рис.3. Параллельное соединение двух индуктивно связанных катушек

Рис.4. Схема двухобмоточного трансформатора

Общие сведения и основные расчётные формулы:

Схема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот, представлена на рис.1, где 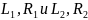– индуктивности и сопротивления соответственно первой и второй катушек; – их взаимная индуктивность.

Степень магнитной связи двух катушек определяется коэффициентом связи:

где – индуктивные сопротивления катушек; –сопротивление взаимной индуктивности; при этом

В режиме гармонических колебаний (в установившемся синусоидальном режиме) уравнения цепи на рис.1 имеют вид:

Знак и определяется выбором положительных направлений токов и . Для выбранных направлений токов , если включение катушек согласное, и , если включение встречное. Ну рис.1 катушки подключены согласованно.

Параметры уравнения могут быть определены из двух опытов холостого хода, в одном из которых , в другом ; осуществляют эти опыты размыканием соответствующей пары внешних выводов катушек. Если используют катушки достаточно высокой добротности ( ), то при определении индуктивностей допустимо пренебречь активными сопротивлениями обмоток катушек, т. е. считать и . Полагая в уравнениях сначала , а затем , при условии получаем соответственно:

На рис.2 показано последовательное соединение двух индуктивно связанных катушек. В этом случае , и из уравнений при находим выражение эквивалентной индуктивности:

Для параллельного соединения (рис.3) , . Разрешая систему уравнений относительно токов с учетом , можно получить выражение эквивалентной индуктивности:

В выражениях для при согласном и при встречном включениях катушек.

Если к выводам второй катушки присоединить нагрузочное сопротивление , получим двухобмоточный трансформатор (рис.4). В трансформаторе энергия от источника, включенного в цепь первичной обмотки, передается нагрузке , подключенной ко вторичной обмотке. Эта передача осуществляется без электрической связи между обмотками посредством изменяющегося потока взаимной индукции.

Рассматривая трансформатор как четырехполюсник, можно его передающие свойства характеризовать функциями передачи напряжений и токов. Положив , из уравнений (9.2) при получаем:

В случае активной нагрузки модуль функции передачи по напряжению (АЧХ)

Обработка результатов

1. Определение индуктивностей катушек, взаимной индуктивности и коэффициента связи

Расчёт параметров катушек, коэффициентов связи и, с целью контроля, при частоте и напряжении ГС .

Таблица №1

№ катушки	U1, В	U2, В	I, мА	x, Ом	L, Гн	Xm, Ом	|M|, Гн
1	1,88	1,37	12,40	151,61	0,0241	110,48	0,0176
2	0,71	1,85	6,50	284,60	0,0450	109,23	0,0173

Расчеты для катушки №1:

Расчёты для катушки 2:

2. Исследование последовательного соединения индуктивно связанных катушек

Частота , напряжение ГС . Для вычисления I, U₁, U₂, L_э используйте рассчитанные в 1 пункте значения L₁, L₂, M; при этом M и X_m примем как среднее из двух значений, определенных в пункте 1.

Таблица №2

Подключение	U, В	U1, В	U2, В	I, мА	I, мА	U1, В	U2, В	Lэ, Гн
Согласное	2	0,76	1,20	3,00	2,62	0,77	1,24	0,12
Встречное	2	0,32	1,55	8,23	7,28	0,33	1,67	0,04

Расчёты для согласного включения:

Расчёты для встречного включения:

3. Исследование параллельного соединения индуктивно связанных катушек

Частота , напряжение ГС .

Таблица №3

Подключение	U, В	I, мА	I, мА	Lэ, Гн
Согласное	0,91	6,56	6,25	0,0255
Встречное	0,41	12,85	17,36	0,00917

Расчёты для согласного включения:

Расчёты для встречного включения:

4. Исследование АЧХ передаточной функции трансформатора по напряжению

Таблица №4

			Опыт	Расчёт				Опыт	Расчёт
0,1	1	0,57	0,57	0,60	1		0,65		0,65	0,62
0,3	1	0,55	0,55	0,47	1		0,72		0,72	0,62
0,6	1	0,43	0,43	0,32	1		0,71		0,71	0,61
0,9	1	0,33	0,33	0,23	1		0,71		0,71	0,60
1,1	1	0,29	0,29	0,19	1		0,7		0,7	0,59
1,4	1	0,22	0,22	0,15	1		0,68		0,68	0,58
4,266	1	0,08	0,08	0,05	1		0,54		0,54	0,40
7,1326	1	0,05	0,05	0,03	1		0,38		0,38	0,28
8,5653	1	0,04	0,04	0,03	1		0,35		0,35	0,24
10	1	0,03	0,03	0,02	1		0,29		0,29	0,21

Пример расчёта для :

Рис.5. АЧХ передаточной функции трансформатора по напряжению при

R_н = 100 Ом

Рис.6. АЧХ передаточной функции трансформатора по напряжению при

R_н = 1000 Ом

Вопрос 1: Как установить правильность выполнения проведенных исследований?

При определении индуктивностей катушек, взаимной индуктивности и коэффициента связи правильность исследования проверяется путем вычисления ; при исследовании последовательного соединения – с помощью уравнений Кирхгофа.

Вопрос 2: Как практически разметить однополярные выводы двух индуктивно-связанных катушек?

Определить согласное включение или встречное можно по величине входного тока при постоянном входном напряжении (поменять выводы одной из катушек местами, сравнить величину тока с предыдущим, при согласном меньше, чем при встречном). Для согласного включения ток должен быть направлен симметрично с однополярными выводами, для встречного – не симметрично.

Вопрос 3: При каком соотношении между параметрами катушек , , напряжение одной из них в режиме гармонических колебаний при последовательном соединении катушек и встречном включении будет отставать от тока?

При последовательном соединении катушек:

С учетом того, что R₁=R₂ = 0 и получаем:

Таким образом, напряжение катушки будет отставать от тока при или

Вопрос 5: Чем объяснить резкое расхождение расчетных и опытных значений при ?

Резкое расхождение в опыте и расчете при объясняется тем, что при расчете мы рассматриваем идеальный трансформатор, а в реальном трансформаторе функция передачи с ограниченной полосой частот, у которой ширина определяется значениями параметров трансформатора.

Вопрос 4: Почему АЧХ трансформатора падает в области низких и высоких частот? В какой частотной области исследуемый трансформатор приближается к идеальному? Почему на нулевой частоте сигнал через трансформатор к нагрузке не проходит?

Вывод: в ходе лабораторной работы были экспериментально определены параметры индуктивности, взаимной индуктивности, индуктивного сопротивления, а также коэффициента связи двух индуктивно связанных катушек. Были проверены основные соотношения индуктивно связанных цепей при параллельном и последовательном соединении катушек. Теоретические и практические расчеты совпадают в пределах допустимой погрешности.

Также был произведет теоретический и практический расчёт АЧХ катушек с подключенной нагрузкой в режиме трансформатора, построены графики для двух величин, сопротивления нагрузки которых 100 и 1000 Ом. Графики примерно показывают тот же результат, но в результате измерений при практическом методе графики находятся выше. Это может быть связано с человеческим фактором.