МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники

отчет по лабораторной работе № 2 по дисциплине «Квантовая и оптическая электроника» Тема: «ИССЛЕДОВАНИЕ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ ТВЕРДОТЕЛЬНОГО ЛАЗЕРА С ДИОДНОЙ НАКАЧКОЙ»

Студенты гр.№1282 ____________________ ____________________ ____________________ . . Преподаватель ____________________ Киселев А.С.

Санкт-Петербург 2024

Лабораторная работа №2 Тема: «исследование генерации второй гармоники твердотельного лазера с диодной накачкой»

Цель работы: исследование процесса нелинейно-оптического формирования второй гармоники твердотельного лазера с накачкой излучением инжекционного полупроводникового лазера.

Основные теоретические положения

Для нелинейной оптики характерна зависимость оптических парамет-ров того или иного вещества от интенсивности падающего излучения. Ти-пичным примером нелинейно-оптического эффекта, который нашел ши-рокое практическое применение, может служить генерация второй гармо-ники лазерного излучения.

Распространение оптического излучения в среде происходит в резуль-тате эффекта переизлучения. Он состоит в том, что при падении внешнего излучения на вещество в области взаимодействия происходит поляризация среды. Ее следствиями являются возникновение собственного излучения среды, поляризация соседних областей, новое собственное излучение среды и т. д. Степень поляризации среды, или электрический дипольный момент, наведенный в среде внешним излучением, определяется диэлек-трической восприимчивостью среды и напряженностью электрического поля Е внешней волны: Р =  Е. При низких уровнях Е (линейная оптика)   f (E). В интенсивных пучках мощных лазеров напряженность световой волны возрастает до уровня напряженности электрического поля атома, что приводит к проявлению зависимости свойств среды от Е. В частности, в этих условиях для изотропной среды диэлектрическая восприимчивость  = f (E) = _I + _II Е + _III Е² + …, где _I, _II, _III – диэлектрические восприимчивости для первой, второй и третьей гармоник соответственно. Тогда выражение Р = _IЕ + + _II Е² + _III Е³ + … будет характеризовать нелинейно-оптический эффект в среде. В зависимости от значений диэлектрических восприимчиво-стей _II, _II среды подразделяют на квадратичные, кубические и т. д. При распространении излучения в квадратичной среде (_II  _III) вдоль оси z излучения основной гармоники c круговой частотой _I = 2_I и скоростью _I степень поляризации определится как

P (t) = _IE₀ cos (_It  z / v_I ) + _II cos² (_It  z / v_I ) =

= _IE₀ cos (_It  z / v_I ) + 0.5_II  1 + cos (2_It 2 z / v_I ) (1)

Таким образом, при воздействии на квадратичную среду интенсивно-го монохроматического, обычно лазерного, излучения с исходной часто-той _I в ней дополнительно может возникнуть вторая гармоника излуче-ния с частотой _II = 2_I.. Условием возможности передачи энергии от первой гармоники ко второй является равенство скоростей их распространения в среде  условие волнового синхронизма v_I = v_II или с / n_I = с / n_II и, следовательно, n_I= n_II, где c  скорость света в вакууме; n_I, n_II  показатели преломления среды для первой и второй гармоник излучения.

Для генерации второй гармоники чаще всего используют одноосные двулучепреломляющие кристаллы, в которых могут существовать “обыкновенный” и “необыкновенный” лучи. Скорость “обыкновенного” луча в кристалле v_о = с / n_о не зависит от направления распространения, характеризуемого углом , что предопределяет зависимость n_о = f () в виде окружности (рисунок 1). Напротив, скорость v_е и показатель преломления n_е “необыкновенного” луча зависят от направления распространения.

Рисунок 1 Волновой синхронизм в одноосном кристалле

Функция n_е = f () имеет вид эллипса, а при  = 0 выполняется равенство n_е = n_о. Для сред с нормальной дисперсией повышение частоты падающего излучения сопровождается ростом показателя преломления. Тогда показатели преломления для вторых гармоник будут выше, чем для первых: и 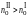. Если свойства кристалла таковы, что окружность и эллипс пересекаются, то имеется такое направление распространения излучения  = _с, при котором и условие волнового синхронизма выполняется.

Состояние волнового синхронизма очень критично направлению распространения: отклонение на единицы градусов от условия  = _с приводит к спаду мощности второй гармоники на 50 %. Для всех нелинейно-оптических кристаллов показатели преломления n_е, n_о являются функциями температуры среды и длины волны (частоты) излучения. В итоге эффективность генерации второй гармоники зависит не только от свойств кристаллов, используемых в качестве нелинейных сред, их геометрии и пространственной ориентации относительно оси лазерного пучка, но и от степени монохроматичности и направленности пучка основной гармоники лазерного излучения.

Как видно из (1), второе слагаемое в функции поляризуемости среды, отвечающее за формирование второй гармоники, сильно квадратично зависит от напряженности электрического поля падающей волны Е. Это означает, что эффективность генерации второй гармоники тем выше, чем больше Е, т. е. чем выше плотность исходного лазерного излучения. Увеличение эффективности генерации второй гармоники при неизменном уровне мощности накачки лазера может быть достигнуто при переходе от непрерывного к импульсному режиму. Наилучшие результаты достигаются в режиме модулированной добротности резонатора, который характеризуется высокой импульсной мощностью лазерного излучения.

Нелинейно-оптическая среда, в которой происходит преобразование основной гармоники во вторую, принципиально может размещаться внутри или вне основного резонатора лазера. Внутрирезонаторное преобразование гармоник более эффективно, так как плотность когерентной мощности, циркулирующей внутри оптического резонатора и воздействующей на нелинейную среду, во много раз выше, чем в выходном излучении лазера. В этом случае генерация второй гармоники имеет высокий КПД преобразования _II, достигающий при оптимальном согласовании десятков процентов.

При расположении нелинейно-оптического кристалла вне резонатора реализуется однопроходное преобразование, а в лазерном пучке за кристаллом присутствуют одновременно и первая, и вторая гармоники. Для повышения эффективности внерезонаторного преобразования применяют фокусировку лазерного пучка. Чтобы не увеличивалась расходимость преобразованного пучка, используют две софокусно расположенные одинаковые линзы, между которыми устанавливают нелинейный кристалл.

Широкое распространение получили преобразователи гармоник на основе нелинейного кристалла титанила фосфата калия (KTiOPO₄, сокращенно KTP), имеющего высокие значения диэлектрической восприимчивости _II для второй гармоники. Помимо KТР для генерации второй гармоники используются также кристаллы дигидрофосфата калия, дигидрофосфата аммония, ниобата лития и др. В настоящее время в импульсных твердотельных лазерах за счет высокой плотности мощности достигнута генерация третьей (борат бария) и четвертой (борат лития) гармоник лазерного излучения.