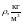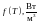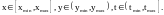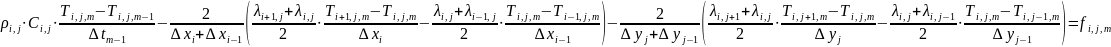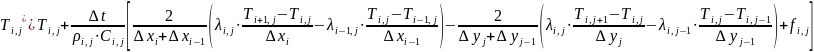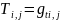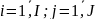МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники |
||||||||||||
отчет по практическому заданию № 2 по дисциплине «Моделирование и проектирование микро- и наносистем» Тема: «Численное моделирование нестационарного процесса теплопроводности в неоднородном теле с учётом зависимости плотности мощности источников (стоков) тепла от температуры с использованием явной схемы» Вариант №2
|
||||||||||||
|
||||||||||||
Санкт-Петербург 2024 |
ИСХОДНЫЕ ДАННЫЕ
Исходные данные для расчетов представлены в таблице 1, вид исследуемой структуры представлен на рисунке 1.
Таблица 1 – Исходные данные для выполнения задания
№ п/п |
L, мм |
W, мм |
Коэффициент теплопроводности
|
Плотность
|
Удельная теплоемкость
|
Начальное и граничные условия (род) |
Зависимость плотности мощности источников (стоков) тепла от температуры
|
Интервал времени t, с |
2 |
50 20 200 |
20 20 20 20 30 30 30 50 50 170 |
1000 10 100 10 100 10 10000 |
10000 2000 1000 2000 1000 2000 300 |
10000 100 1000 100 1000 100 300 |
300(1) 0(2) 0(2) 300(1) 300(1) |
5·108/(T-273) |
10 |
Рисунок 1 – Общий вид неоднородной структуры
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Дифференциальное уравнение теплопроводности для нестационарного случая с начальным и граничными условиями задается системой (1):
|
(1) |
При этом две пространственные и одна временная переменные принимают значения (2):
|
(2) |
Конечно-разностное представление ДУ нестационарной задачи теплопроводности:
|
|
Запишем уравнение, выражающее данные через несколько соседних точек результата для явной схемы:
Начальное условие:
Граничные условия:
|
|
В итоге получаем систему (3):
|
(3) |
Дискретная
задача будет решаться с помощью явной
схемы: на дискретизированном пространстве
строится равномерная (сетка может быть
и неравномерной, как в нашем случае)
прямоугольная сетка, на которой искомое
значение функции
будет
находиться с использованием имеющихся
значений
,
,
.
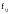То есть значения j-го
слоя формируют значения j+1-го
слоя. При этом переменные i
и j
изменяются в пределах от 2 до I-1
и от 2 до J-1
соответственно. Значения при i
и j,
равных 1 и I
или J,
определяются граничными условиями. В
явном виде это может представить как
соотношения (4).
|
(4) |
где τ – шаг сетки по координате, за которую отвечает переменная j, h – шаг сетки по координате, за которую отвечает переменная i.
С помощью метода гармоник можно показать необходимое и достаточное условие устойчивости явной схемы. Из этого метода делается вывод, что для уравнения теплопроводности условие устойчивости выполняется в случае выполнения неравенства (5):
|
(5) |
где a – коэффициент температуропроводности, см2/с.
Таким образом, явная схема для уравнения теплопроводности условно устойчива.
Дискретная система в случае решения уравнения теплопроводности с помощью явной схемы может быть записана в виде выражения (6):
|
(6) |
РАСЧЕТНАЯ ЧАСТЬ
Полученные результаты моделирования представим на рисунках 2 – 12.
Рисунок 2 – Распределение температуры в пространстве в момент времени t = 0 секунд
Рисунок 3 – Распределение температуры в пространстве в момент времени t = 1 секунды
Рисунок 4 – Распределение температуры в пространстве в момент времени t = 2 секунды
Рисунок 5 – Распределение температуры в пространстве в момент времени t = 3 секунды
Рисунок 6 – Распределение температуры в пространстве в момент времени t = 4 секунд
Рисунок 7 – Распределение температуры в пространстве в момент времени t = 5 секунд
Рисунок 8 – Распределение температуры в пространстве в момент времени t = 6 секунд
Рисунок 9 – Распределение температуры в пространстве в момент времени t = 7 секунд
Рисунок 10 – Распределение температуры в пространстве в момент времени t = 8 секунд
Рисунок 11 – Распределение температуры в пространстве в момент времени t =9 секунд
Рисунок 12 – Распределение температуры в пространстве в момент времени t = 10 секунд
КОД ПРОГРАММЫ
clear all
close all
clc
L=[50 20 200];
W=[20 20 20 20 30 30 30 50 50 170];
L=L.*1e-3;
L(3)=L(3)-L(1)-L(2);
W=W.*1e-3;
kM=[1000 10 100 10 100 10 10000];
rM=[10000 2000 1000 2000 1000 2000 300];
cM=[10000 100 1000 100 1000 100 300];
gt=300;
gxmin=0;
gxmax=0;
gymin=300;
gymax=300;
GrStep=1e5;
NG='Figure_';
tmax=10;
F=5e8;
Sx=5;
Sy=7;
t=0;
dt=1e-5;
x(1)=0;
kL(1)=kM(1);
rL(1)=rM(1);
cL(1)=cM(1);
for i=1:length(kM)
x=[x max(x)+W(i)/Sx:W(i)/Sx:max(x)+W(i)];
kL=[kL ones(1,Sx).*kM(i)];
rL=[rL ones(1,Sx).*rM(i)];
cL=[cL ones(1,Sx).*cM(i)];
end
kL=kL';
rL=rL';
cL=cL';
I=length(x);
dx=diff(x);
y(1)=0;
for i=1:length(L)
y=[y max(y)+L(i)/Sy:L(i)/Sy:max(y)+L(i)];
end
J=length(y);
dy=diff(y);
k=kL;
c=cL;
r=rL;
for j=2:J
k=[k kL];
c=[c cL];
r=[r rL];
end
T=ones(I,J).*gt;
f=zeros(I,J);
ct=0;
ctt=0;
NG='Fig 1';
NameofG=[NG num2str(ctt)];
mesh(y.*1e3,x.*1e3,T-273);
xlabel('y, mm', 'FontSize', 19);
ylabel('x, mm', 'FontSize', 19);
zlabel('T, ^oC', 'FontSize', 19);
xlim([min(y.*1e3) max(y.*1e3)]);
ylim([min(x.*1e3) max(x.*1e3)]);
zlim([27 100]);
colormap([0 0 0]);
grid on;
set(gcf,'Position',[197, 42, 826, 642]);
print(gcf, '-djpeg', NameofG);
pause(1e-3)
while t<=tmax
t=t+dt;
ct=ct+1;
for j=Sy+1:2*Sy+1
for i=1:I
if x(i)>=W(9) && x(i)<=W(9)+W(8)
f(i,j)=F/(T(i,j)-273);
end
end
end
for j=2:J-1
TT(I,j)=T(I-1,j)+dx(I-1)*gxmax;
TT(1,j)=T(2,j)-dx(1)*gxmin;
end
for i=1:I
TT(i,1)=gymin;
TT(i,J)=gymax;
end
for i=2:I-1
for j=2:J-1
TT(i,j)=T(i,j)+...
(2/(dx(i)+dx(i-1))*(k(i,j)*(T(i+1,j)-T(i,j))/dx(i)-...
k(i-1,j)*(T(i,j)-T(i-1,j))/dx(i-1))+...
2/(dy(j)+dy(j-1))*(k(i,j)*(T(i,j+1)-T(i,j))/dy(j)-...
k(i,j-1)*(T(i,j)-T(i,j-1))/dy(j-1))+...
f(i,j))*dt/r(i,j)/c(i,j);
end
end
if mod(ct,GrStep)==0
ctt=ctt+1;
NameofG=[NG num2str(ctt)];
figure
mesh (y.*1e3,x.*1e3,TT-273)
xlabel('y, mm','FontSize',19)
ylabel('x, mm','FontSize',19)
zlabel('T, ^oC','FontSize',19)
xlim ([min(y*1e3) max(y*1e3)])
ylim ([min(x*1e3) max(x*1e3)])
zlim([27 100]);
grid on
colormap([0 0 0])
clc
set(gcf,'Position',[197, 42, 826, 642]);
print(gcf,'-djpeg',NameofG)
end
T=TT;
end
ВЫВОД
В ходе выполнения лабораторной работы был использован сеточный метод решения системы линейных алгебраических уравнений теплопроводности с помощью явной схемы. Преимуществами данного метода являются быстродействие и значительная экономия оперативной памяти, что позволяет решать сложные комплексные задачи, сохраняя только значения для предыдущего момента времени. Этот метод вычисления представляет собой удобный подход, т.к. температурное поле в каждой координате для каждого временного момента рассчитывается последовательно в циклах, что способствует снижению объема используемой оперативной памяти. При применении явной схемы для обеспечения корректности расчетов необходимо согласовывать интервалы по координатам и времени, чтобы соблюдать условия устойчивости (то есть схема будет работать только при соблюдении определенного условия). Можно сказать, что это ее основной недостаток.