МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физической электроники и технологии
отчет
по лабораторной работе № 5
по дисциплине «Электродинамика»
Тема: «Исследование широкополосного согласования сопротивления нагрузки и СВЧ-генератора»
Студенты гр. №1282 |
____________________ ____________________ ____________________
|
Ибрагимов М.А. Пискунов В.М. Матгафуров Н.И. |
Преподаватель |
__________________________ |
Платонов Р.А. |
Санкт-Петербург
2023
ЦЕЛЬ: расчет схемы согласующего тракта на основе микрополосковой линии передачи, обеспечивающего широкополосное согласование источника СВЧ-сигнала и нагрузки.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Согласование сопротивлений является одной из важнейших задач техники СВЧ и заключается в обеспечении наиболее эффективной передачи сигнала из источника СВЧ-мощности в полезную нагрузку, в условиях, когда их сопротивления различны. Такое различие сопротивлений нагрузки и источника ведёт к отражению части падающей мощности, и, следовательно, к снижению эффективности передачи. Задача согласования в общем случае может быть решена созданием согласующих схем на основе активных и реактивных сосредоточенных элементов, а применительно к СВЧ – на основе трансформаторов сопротивлений, разработанных с использованием теории длинных линий. Согласование нагрузки и подводящей линии передачи, имеющих сопротивления Zн и Zл соответственно, может быть выполнено с помощью λ/4 (четвертьволнового) трансформатора. Трансформатор представляет собой одиночный отрезок или последовательное соединение N отрезков линии передачи, длина каждого их которых равна λ/4 (электрическая длина – π/2), где λ – длина волны в данном отрезке линии передачи, а сопротивление каждого из которых Zтр,n (n = 1,2…N) рассчитывается с использованием телеграфных уравнений.
Для линии передачи (с пренебрежимо малыми потерями) длиной l с характеристическим сопротивлением Z0, нагруженной на сопротивление Zн (рисунок 1), справедлива формула трансформации сопротивлений – формула 1
|
(1) |
где
 – постоянная распространения.
– постоянная распространения.
Когда длина линии равна l = λ/4, выражение (1) упрощается до (2):
|
(2) |
Из выражения (2) видно, что в сопротивление нагрузки может быть трансформировано в сопротивление подводящей линии передачи с помощью отрезка длиной λ /4, сопротивление которого Zтр находится заменой Zвх на Zл в выражении (2) как (3):
|
(3) |
Из условия вывода выражения (2) видно, что полное согласование с помощью одиночного отрезка достигается на единственной частоте f0, для которой λ/4 = l. Во многих случаях уровень рассогласования, вызванный отклонением частоты от заданного значения, недопустим. Поэтому возникает задача широкополосного согласования, при котором обеспечивается полоса частот, в пределах которой отражение не превышает заданного значения. Эта задача решается применением многоступенчатого λ/4-трансформатора.

Рисунок 1 – Схема линии передач с малыми потерями и сопротивлением нагрузки
Теория длинных линий показывает, что при двухкаскадном (N = 2) соединении трансформаторов (рисунок 2) волновые сопротивления каждого из них могут быть определены, исходя из следующих соотношений (4)
|
(4) |

Рисунок 2 – Схема двухкаскадного соединения трансформаторов
В интегральных схемах СВЧ используются планарные линии передачи, плоские проводники которых формируются на поверхности диэлектрической подложки методами интегральной технологии с применением фотолитографии для получения необходимого рисунка топологии. Наибольшее применение нашла микрополосковая линия (МПЛ), поперечное сечение которой представлено на рисунке 3. МПЛ относится к категории линий со слоистым диэлектриком, для которых вводится понятие эффективной диэлектрической проницаемости, учитывающей то, что часть поля находится в диэлектрике, а часть – в воздухе. Эффективная проницаемость такой линии передачи определяется из отношения длины волны в свободном пространстве λ0 = с/f на частоте fк длине волны в линии передачиλ на той же частоте f: εэф = (λ0/λ)2. Введение εэф позволяет описывать рассматриваемую линию как некоторую эквивалентную, имеющую такие же геометрические размеры, но однородное диэлектрическое заполнение.

Рисунок 3 – Поперечное сечение микрополосковой линии передач


ОБРАБОТКА РЕЗУЛЬТАТОВ
Исходные данные для 2 варианта
№ Варианта |
|
|
|
|
2 |
30 |
3 |
1 |
4 |
Расчет волновых сопротивлений и геометрических параметров согласующихся цепей проводится исходя из формул (3), (4), (5.5…5.7). Рассчитанные параметры цепей представлены в таблице 1. Код для автоматического расчета в программе Mathcad представлен на рисунке 4.
Для простой линии передачи (n = 1)



Тогда ширина полоска так как А < 1.52
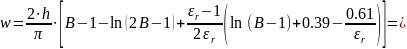
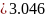 мм
мм
Эффективная диэлектрическая проницаемость для полученной ширины

Что бы найти длину линии передачи необходимо определить длину волны на частоте согласования

И длина линии

Для двухкаскадной линии передачи (n = 2)






Тогда ширины полосков так как А1, 2 < 1.52

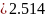 мм
мм

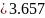 мм
мм
Эффективная диэлектрическая проницаемость для полученной ширины


Что бы найти длину линии передачи необходимо определить длину волн на частоте согласования

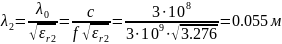
Тогда длины соответствующих полосков


Таблица 1 – Рассчитанные параметры цепей
Вид цепи |
Zтр, Ом |
w, мм |
l, мм |
Одноэлементная |
38,73 |
3,046 |
16 |
Двухэлементная |
|
|
|

Рисунок 4 – Программа ПО Mathcad для расчета параметров двух согласующихся цепей
Схемные модели однокаскадного и двухкаскадного четвертьволнового трансформатора представлены на рисунках 5, 6 соответственно.
Результаты моделирования частотных зависимостей коэффициента отражения для одноэлементной и двухэлементной согласующих цепей представлены в декартовой системе координат (рисунки 7, 8).

Рисунок 5 – Схема однокаскадного четвертьволнового трансформатора

Рисунок 6 – Схема двухкаскадного четвертьволнового трансформатора

Рисунок 7 – Частотная зависимость коэффициента отражения для однокаскадной схемы

Рисунок 8 – Частотная зависимость коэффициента отражения для двухкаскадной схемы
ВЫВОД
Главной задачей работы был расчет и анализ цепей согласования для СВЧ источника и нагрузки. В результате расчета и моделирования двух разных схем согласования, можно сделать вывод, что согласования с помощью одного отрезка, то есть с использованием однокаскадного четвертьволнового трансформатора обеспечивает наименьшее отражение мощности, а значит и наибольшую эффективность передачи, однако очень чувствительно к отклонению частоты от частоты согласования, в таком случае эффективность резко снижается (рисунок 7). Данную проблему можно решить, используя многокаскадные линии передачи, в которых широкая полоса пропускания частот (рисунок 8). В таком случае диапазон частот согласования увеличивается, но коэффициент отражения немного выше, чем в случае одного каскада.