МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
отчёт
по индивидуальному заданию №4
по дисциплине «Моделирование и проектирование микро- и наносистем»
Тема: Численное решение фундаментальной системы уравнений полупроводника в диффузионно-дрейфовом приближении для моделирования стационарных процессов в p-n-переходе
Вариант №4
Студент гр. |
|
:P bleh :P |
Преподаватель |
|
Рындин Е. А. |
Санкт-Петербург
2025
Цель работы.
Численное моделирование стационарных процессов в p-n-переходе. Построение вольт-амперной характеристики (ВАХ) и пространственных распределений электростатического потенциала и концентраций электронов и дырок для каждой точки ВАХ полупроводникового р-n-перехода.
Задание.
Таблица 1 - Исходные данные
№ п/п |
Полупроводник |
Длина n-области Ln, нм |
Длина p-области Lp, нм |
Концентрация легирующей примеси в n-области ND, см-3 |
Концентрация легирующей примеси в p-области NA, см-3 |
Диапазон напряжений U, В |
Температура кристалла T, К |
4. |
Кремний (Si) |
250 |
200 |
1 * 1017 |
3 * 1017 |
0 – 0,7 |
300 |
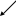
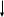
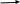
n - область
p - область
x
y
z
xmax
xmin
Рис. 1 – Общий вид полупроводниковой структуры
Теоретические положения.
Ⅰ. Система уравнений и граничные условия в обычном виде, без нормировки:
Данная система состоит из уравнения Пуассона, которое описывает распределение потенциала в кристалле, и уравнений непрерывности для концентраций электронов и дырок.
Граничные условия для концентраций:
Граничные условия для потенциала:
→
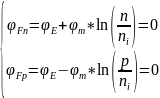Порядки расчётных величин могут сильно различаться, поэтому далее проводится нормировка. Разница между концентрациями без нормировки – 25 порядков; с нормировкой – 6 порядков. Без нормировки погрешность на разярдной сетке компьютера будет намного больше.
Таблица 2 – Данные для нормировки |
|
Нормируемая величина |
Нормирующий коэффициент |
x |
L0
=
|
t |
|
φ, U |
φт
=
|
n, p, N |
ni |
μn, μp |
μ0
=
|
jn, jp |
j0
=
|
n =
*ni,
p =
*ni,
φ =
*φт,
x =
*L0
Для удобства переобозначим: → n, → p, → φ, → x
Ⅱ. Система уравнений и граничные условия в обычном виде с учётом нормировки:
Граничные условия для концентраций и потенциала:
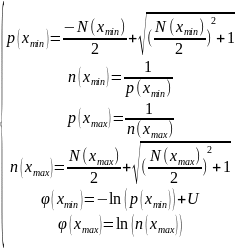
Из базиса
перейдём в базис Слодбума
для улучшения сходимости, где:
→
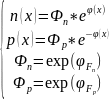- нормированная
система уравнений в новом базисе.
Граничные условия для концентраций и потенциала в новом базисе:
Ⅲ. Система уравнений и граничные условия в дискретном виде с учётом нормировки:
,
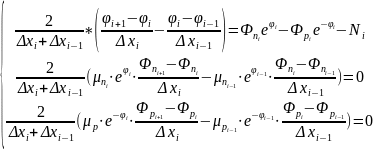где
I = 2…I – 1
,
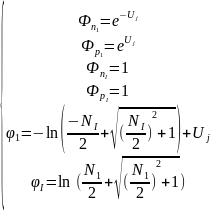где j
= 1…J
Для решения данной системы может использоваться 2 итерационных метода: Гуммеля и Ньютона-Рафсона. Рассмотрим метод Гуммеля:
1) задается начальная
невязка
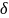
2) задаётся начальное
приближение
(например, линейное приближение
)
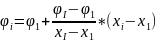и подставляется в уравнение непрерывности
3) решается система уравнений относительно экспонент квазиуровней Ферми с учётом начального приближения
4) по полученным
значениям ищется следующее приближение
5) по полученному ищется текущая невязка и сравнивается с заданным значением; если текущая невязка больше, чем заданная, то наступает следующий шаг итерации; если же заданная невязка больше, чем текущая, то расчет останавливается и полученные значения искомых величин выводятся на экран.
Оценка приближения к решению (невязка):
=
Код был написан в программе Matlab и, конкретно для этого задания, поделен на несколько файлов. Для удобства поместим весь код в один файл:
clear all
close all
clc
warning off
%prog_parameters
LW=2; %толщина линий для графиков
FS=19; %размер шрифта
Sx=100;
Delta=1e-6;
%constants
q=1.6e-19;
eps0=8.85e-12;
h=6.6262e-34;
kB=1.38e-23;
me=9.1e-31;
%initial_data
T=300;
eps=11;
W=[200 250];
W=W.*1e-9;
ND=[1e14 1e17].*1e6;
NA=[3e17 1e14].*1e6;
Nef=ND-NA;
VAH=menu('IV direction','Forvard','Reverse');
if VAH==1
U=[0 0.1 0.2 0.3 0.4 0.45 0.5 0.52 0.54 0.56 0.58 0.6 0.62 0.64 0.66 0.67 0.68 0.69 0.7];
K=[55 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50];
else
U=[0 -0.01 -0.02 -0.03 -0.04 -0.05 -0.07 -0.1 -0.2 -0.3 -0.4 -0.5 -0.6 -0.7];
K=[40 40 40 40 40 40 40 40 40 40 40 40 40 35];
end
%parameters
ft=kB*T/q;
Eg0=1.1695;
Alfa=4.73e-4;
Betta=636;
Eg=Eg0-Alfa*T^2/(Betta+T);
mnt=0.19;
mnl=0.98;
m1n=0.009;
mpl=0.16;
mph=0.49;
m1p=0.6;
m2p=-0.1;
m0n=(mnt^2*mnl)^(1/3);
m0p=(mpl^1.5+mph^1.5)^(2/3);
mn=m0n+m1n*(T/300);
mp=m0p+m1p*(T/300)+m2p*(T/300)^2;
Nc=2*(2*pi*mn*me*kB*T/h^2)^1.5;
Nv=2*(2*pi*mp*me*kB*T/h^2)^1.5;
ni=sqrt(Nc*Nv)*exp(-Eg/2/ft);
muL300n=1430*1e-4;
muL300p=460*1e-4;
g0n=-2;
g0p=-2.18;
g1n=-0.45;
g1p=-0.45;
g3n=3.2;
g3p=3.2;
g4n=0.065;
g4p=0.065;
muMin300n=80*1e-4;
muMin300p=45*1e-4;
Cref300n=1.12e17*1e6;
Cref300p=2.23e17*1e6;
a300n=0.72;
a300p=0.72;
muLn=muL300n*(T/300)^g0n;
muLp=muL300p*(T/300)^g0p;
muMinn=muMin300n*(T/300)^g1n;
muMinp=muMin300p*(T/300)^g1p;
Crefn=Cref300n*(T/300)^g3n;
Crefp=Cref300p*(T/300)^g3p;
an=a300n*(T/300)^g4n;
ap=a300p*(T/300)^g4p;
MUn=muMinn+(muLn-muMinn)./(1+((ND+NA)./Crefn).^an);
MUp=muMinp+(muLp-muMinp)./(1+((ND+NA)./Crefp).^ap);
%grid_functions
x(1)=0;
N(1)=Nef(1);
Mun(1)=MUn(1);
Mup(1)=MUp(1);
for i=1:length(W)
x=[x max(x)+W(i)/Sx:W(i)/Sx:max(x)+W(i)];
N=[N ones(1,Sx).*Nef(i)];
Mun=[Mun ones(1,Sx).*MUn(i)];
Mup=[Mup ones(1,Sx).*MUp(i)];
end
I=length(x);
dx=diff(x);
x=x';
dx=dx';
N=N';
Mun=Mun';
Mup=Mup';
%normirovka
t0=1e-6;
N0=ni;
V0=ft;
L0=sqrt(2*eps*eps0*V0/q/N0);
MU0=L0^2/V0/t0;
E0=V0/L0;
J0=q*N0*L0/t0;
x=x./L0;
dx=dx./L0;
N=N./N0;
mun=Mun./MU0;
mup=Mup./MU0;
U=U./V0;
%initial_approx
fi0(1)=-log(-N(1)/2+sqrt((N(1)/2)^2+1))+U(1);
fi0(I)=log(N(I)/2+sqrt((N(I)/2)^2+1));
for i=2:I-1
fi0(i)=(fi0(I)-fi0(1))/(x(I)-x(1))*(x(i)-x(1))+fi0(1);
end
fi0=fi0';
for j=1:length(U)
if j>1
%initial_approx_U
fi0(1)=-log(-N(1)/2+sqrt((N(1)/2)^2+1))+U(j);
fi0(I)=log(N(I)/2+sqrt((N(I)/2)^2+1));
for i=2:I-1
fi0(i)=fi0(i)+(fi0(I)-fi0(i))/(fi0(I)-fi0(1))*(U(j)-U(j-1));
end
end
err=10*Delta;
ct=0;
while err>Delta
ct=ct+1;
if j==1
Fn=ones(I,1);
Fp=ones(I,1);
else
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=exp(-U(j));
A(I,I)=1;
B(I)=1;
for i=2:I-1
A(i,i)=-mun(i)*exp(fi0(i))/dx(i)-mun(i-1)*exp(fi0(i-1))/dx(i-1);
A(i,i+1)=mun(i)*exp(fi0(i))/dx(i);
A(i,i-1)=mun(i-1)*exp(fi0(i-1))/dx(i-1);
B(i)=0;
end
Fn=A^(-1)*B;
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=exp(U(j));
A(I,I)=1;
B(I)=1;
for i=2:I-1
A(i,i)=-mup(i)*exp(-fi0(i))/dx(i)-mup(i-1)*exp(-fi0(i-1))/dx(i-1);
A(i,i+1)=mup(i)*exp(-fi0(i))/dx(i);
A(i,i-1)=mup(i-1)*exp(-fi0(i-1))/dx(i-1);
B(i)=0;
end
Fp=A^(-1)*B;
end
A=zeros(I,I);
B=zeros(I,1);
A(1,1)=1;
B(1)=-log(-N(1)/2+sqrt((N(1)/2)^2+1))+U(j);
A(I,I)=1;
B(I)=log(N(I)/2+sqrt((N(I)/2)^2+1));
for i=2:I-1
A(i,i)=2/(dx(i)+dx(i-1))*(-1/dx(i)-1/dx(i-1));
A(i,i+1)=2/(dx(i)+dx(i-1))/dx(i);
A(i,i-1)=2/(dx(i)+dx(i-1))/dx(i-1);
B(i)=Fn(i)*exp(fi0(i))-Fp(i)*exp(-fi0(i))-N(i);
end
fi=A^(-1)*B;
clc
ct
voltage=U(j)*ft
err=max(abs(fi-fi0))/max(abs(fi0))
pause(1e-3)
fi0=fi0+(fi-fi0)./K(j);
n=Fn.*exp(fi0);
p=Fp.*exp(-fi0);
for i=1:I-1
E(i)=-(fi0(i+1)-fi0(i))/dx(i);
end
E(I)=E(I-1)+(E(I-1)-E(I-2));
ro=(p-n+N).*(N0*q);
end
for i=2:I
Jn(i)=mun(i-1)*exp(fi0(i-1))*(Fn(i)-Fn(i-1))/dx(i-1); %берем центральную разность, т.к. погрешность с ней чуть меньше
Jp(i)=-mup(i-1)*exp(-fi0(i-1))*(Fp(i)-Fp(i-1))/dx(i-1);
end
%чтобы показать большую погрешность когда решаем в основном базисе:
%for i=2:I-1
%JnDR(i)=-(mun(i)*n(i)+mun(i-1)*n(i-1))/2*(fi0(i+1)-fi0(i-1))/(dx(i)+dx(i-1));
%JnDF(i)=(mun(i)+mun(i-1))/2*(n(i+1)-n(i-1))/(dx(i)+dx(i-1));
%JpDR(i)=-(mup(i)*p(i)+mup(i-1)*p(i-1))/2*(fi0(i+1)-fi0(i-1))/(dx(i)+dx(i-1));
%JpDF(i)=(mup(i)+mup(i-1))/2*(p(i+1)-p(i-1))/(dx(i)+dx(i-1));
%end
Jn(1)=Jn(2);
Jn(1)=Jn(2);
Jp(1)=Jp(2);
Jp(1)=Jp(2);
%JnDR(1)=JnDR(2);
%JnDF(1)=JnDF(2);
%JpDR(1)=JpDR(2);
%JpDF(1)=JpDF(2);
%JnDR(I)=JnDR(I-1);
%JnDF(I)=JnDF(I-1);
%JpDR(I)=JpDR(I-1);
%JpDF(I)=JpDF(I-1);
%Jn=JnDR+JnDF;
%Jp=JpDR+JpDF;
Js=Jn+Jp;
if VAH==1
Current(j)=Js(I); % для прямой ветви ВАХ
else
Current(j)=Js(fix(I/1.8)); %для обратной ветви ВАХ
end
%graphics
if VAH==1
NN='Point_IV_F';
else
NN='Point_IV_R';
end
subplot(2,3,1)
plot(x.*(L0*1e9),-fi0.*V0+Eg/2,x.*(L0*1e9),-fi0.*V0-Eg/2,x.*(L0*1e9),-fi0.*V0,'--','LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Band diagram, eV','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,2)
plot(x.*(L0*1e9),n.*(N0*1e-6),x.*(L0*1e9),p.*(N0*1e-6),'LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Carrier density, cm^-^3','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
legend('n','p','Location','best')
grid on
subplot(2,3,3)
semilogy(x.*(L0*1e9),n.*(N0*1e-6),x.*(L0*1e9),p.*(N0*1e-6),'LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Carrier density, cm^-^3','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
legend('n','p','Location','best')
grid on
subplot(2,3,4)
plot(x.*(L0*1e9),E.*(E0*1e-2),'LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Electric field, V/cm','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,5)
plot(x.*(L0*1e9),ro,'LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Charge density, uC/cm','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
grid on
subplot(2,3,6)
plot(x.*(L0*1e9),Jn.*(J0*1e-4),x.*(L0*1e9),Jp.*(J0*1e-4), x.*(L0*1e9),Js.*(J0*1e-4),'LineWidth',LW)
xlabel('Coordinate, nm','FontSize', FS)
ylabel('Current density, A/cm^2','FontSize', FS)
xlim([min(x.*(L0*1e9)) max(x.*(L0*1e9))])
legend('J_N','J_P','J_S', 'Location','best')
grid on
set(gcf,'Position',[18.6000 78.6000 1.4712e+03 679.2000])
NNN=[NN num2str(j)];
print(gcf,'-djpeg',NNN)
end
figure
plot(U.*ft, Current.*(J0*1e-4), 'LineWidth',LW)
xlabel('Voltage, V', 'FontSize', FS)
ylabel('Current desity, A/cm^2', 'FontSize', FS)
grid on
%для обратной ветви возьмем середину х, для прямой конец х
if VAH==1
print(gcf,'-djpeg','IV-charact_F');
else
print(gcf,'-djpeg','IV-charact_R');
end