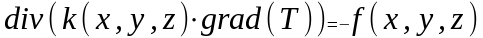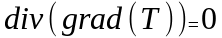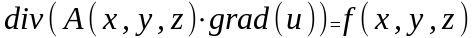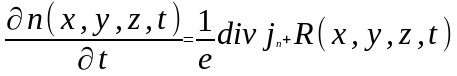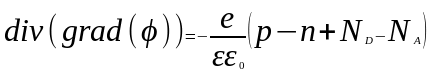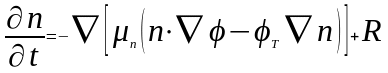- •Фонды оценочных средств по дисциплине «Моделирование и проектирование микро- и наносистем»
- •График текущего контроля успеваемости
- •Методика текущего контроля
- •1. Методика текущего контроля на лекционных занятиях
- •2. Методика текущего контроля на практических занятиях
- •3. Методика текущего контроля самостоятельной работы студентов
- •Фос текущего контроля Темы и варианты для выполнения практических занятий
- •Содержание отчета о выполнении практических занятий
- •Варианты заданий для выполнения практических занятий
- •Примерные вопросы для защиты практических занятий
- •Дифференцированный зачет по результатам текущего контроля
- •Фонды оценочных средств проверки степени сформированности компетенций
Примерные вопросы для защиты практических занятий
1. Запишите результат дискретизации производной первого порядка
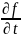 функции f(x,y,t)
на заданном шаблоне.
функции f(x,y,t)
на заданном шаблоне.2. Запишите результат дискретизации производной второго порядка
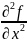 функции f(x,y,t)
на заданном шаблоне.
функции f(x,y,t)
на заданном шаблоне.3. Опишите, чем отличаются явная и неявная схемы численного решения нестационарной задачи теплопроводности.
4. Опишите алгоритм численного решения нестационарной задачи теплопроводности по явной схеме.
5. Опишите алгоритм численного решения нестационарной задачи теплопроводности по неявной схеме.
6. Покажите в исходном тексте программы численного решения нестационарной задачи теплопроводности модуль решения СЛАУ прямым методом.
7. Покажите в исходном тексте программы численного решения нестационарной задачи теплопроводности модуль пересчета сеточной функции плотности мощности источников (стоков) тепла в процессе итерационных процедур.
8. Покажите в исходном тексте программы численного решения нестационарной задачи теплопроводности операцию вычисления невязки.
9. Покажите в исходном тексте программы численного решения нестационарной задачи теплопроводности модуль описания граничных условий первого рода.
10. Покажите в исходном тексте программы численного решения нестационарной задачи теплопроводности модуль описания граничных условий второго рода.
Дифференцированный зачет по результатам текущего контроля
Промежуточная аттестация в виде дифференцированного зачета производится при выполнении всех минимальных показателей текущего контроля:
- посещаемость лекционных занятий не ниже 80%;
- посещаемость практических занятий не ниже 80%;
- выполнение и защита 4 практических занятий с оценкой не ниже «Удовлетворительно» по каждому практическому занятию.
Оценка по дифференцированному зачету определяется средней оценкой по результатам выполнения и защиты 4 практических занятий.
Фонды оценочных средств проверки степени сформированности компетенций
ФОС предназначены для проверки сформированности компетенций после окончания периода обучения по дисциплине «Моделирование и проектирование микро- и наносистем» и представляют собой тесты с вариантами ответов.
Степень сформированности компетенций обучающихся оценивается в соответствии с «Положением о контроле степени сформированности компетенций в СПбГЭТУ «ЛЭТИ» (Приказ № 2283 от 06.07.17).
Правильные ответы на 90% и более вопросов соответствуют высокому уровню освоения компетенций, 70-90% – хорошему, 50-70% – достаточному.
Вопросы для проверки степени сформированности компетенции «Способен проводить физико-математическое моделирование исследуемых процессов нанотехнологии и объектов нано- и микросистемной техники с использованием современных компьютерных технологий (ПК-1)».
1. Запишите уравнение Лапласа для задачи электростатики.
2. Запишите уравнение Пуассона для задачи электростатики.
3. Запишите уравнение теплопроводности.
4. Запишите уравнение диффузии.
5. Запишите волновое уравнение, описывающее незатухающие колебания в среде.
6. Какие граничные условия называются граничными условиями первого рода (условиями Дирихле)?
7. Какие граничные условия называются граничными условиями второго рода (условиями Неймана)?
8. Какие граничные условия называются граничными условиями третьего рода (обобщенными условиями Неймана)?
9. Что такое начальное условие?
10. Какие координатные сетки называются прямоугольными?
11. Какие координатные сетки называются триангулярными?
12. Какие прямоугольные координатные сетки называются равномерными, а какие неравномерными?
13. Что называется ячейкой Дирихле?
14. Какие точки триангулярной сетки называются соседними в смысле Дирихле?
15. Сформулируйте одну из двух теорем, характеризующих отличительные особенности триангуляции Делоне от прочих триангуляций на заданном множестве точек сетки.
Тесты для проверки индикатора ПК-1.1 «Знает физические и математические законы и модели физических процессов, лежащих в основе принципов действия объектов нанотехнологии и микросистемной техники».
Вопрос |
Варианты ответа |
Проверяемые знания |
1. Дифференциальные уравнения в частных производных называют эллиптическими, если дискриминант… ОТВЕТ: 3 |
1. Больше нуля |
Физические и математические законы и модели физических процессов |
2. Равен нулю |
||
3. Меньше нуля |
||
2. Дифференциальные уравнения в частных производных называют гиперболическими, если дискриминант… ОТВЕТ: 1 |
1. Больше нуля |
Физические и математические законы и модели физических процессов |
2. Равен нулю |
||
3. Меньше нуля |
||
3. Дифференциальные уравнения в частных производных называют параболическими, если дискриминант… ОТВЕТ: 2 |
1. Больше нуля |
Физические и математические законы и модели физических процессов |
2. Равен нулю |
||
3. Меньше нуля |
||
4. Уравнение Лапласа является… ОТВЕТ: 3 |
1. Параболическим |
Физические и математические законы и модели физических процессов |
2. Гиперболическим |
||
3. Эллиптическим |
||
5. Задача о нестационарном распределении по координатам концентрации частиц в твердом теле описывается уравнением… ОТВЕТ: 2 |
1. Теплопроводности |
Физические и математические законы и модели физических процессов |
2. Диффузии |
||
3. Пуассона |
||
6. Уравнение вида
где u(x,t) – искомая функция; x – координаты граничных точек области решения задачи, является… ОТВЕТ: 1 |
1. Граничным условием 3-го рода |
Физические и математические законы и модели физических процессов |
2. Граничным условием 2-го рода |
||
3. Граничным условием 1-го рода |
||
7. Левая конечная разность для сеточной функции fi,j,k описывается выражением… ОТВЕТ: 2 |
1.
|
Физические и математические законы и модели физических процессов |
2.
|
||
3.
|
||
8. Конечная разность второго порядка для сеточной функции fi,j,k описывается выражением… ОТВЕТ: 3 |
1. |
Физические и математические законы и модели физических процессов |
2.
|
||
3.
|
||
9. Для координатной сетки
|
1. Ячейкой Дирихле |
Физические и математические законы и модели физических процессов |
2. Элементом триангуляции Делоне |
||
3. Конечным элементом |
||
10. Две точки сетки называются соседними в смысле Дирихле тогда и только тогда, когда многоугольники Дирихле, содержащие эти точки… ОТВЕТ: 2 |
1. Имеют общую грань нулевой длины |
Физические и математические законы и модели физических процессов |
2. Имеют общую грань ненулевой длины |
||
3. Не пересекаются |
Тесты для проверки индикатора ПК-1.2 «Умеет решать задачи, использовать математический аппарат и численные методы компьютерного моделирования объектов нанотехнологии и микросистемной техники».
Вопрос |
Варианты ответа |
Проверяемые знания |
1. Прямым методом решения систем линейных алгебраических уравнений является … ОТВЕТ: 3 |
1. Итерация Якоби |
Математический аппарат и численные методы компьютерного моделирования |
2. Итерация Гаусса-Зейделя |
||
3. Метод исключения Гаусса |
||
2. Матрица коэффициентов СЛАУ называется строго диагонально доминирующей, если … ОТВЕТ: 2 |
1. Модуль элемента главной диагонали любой строки равен сумме модулей остальных элементов данной строки |
Математический аппарат и численные методы компьютерного моделирования |
2. Модуль элемента главной диагонали любой строки больше суммы модулей остальных элементов данной строки |
||
3. Модуль элемента главной диагонали любой строки меньше суммы модулей остальных элементов данной строки |
||
3. Метод Ньютона-Рафсона предполагает использование следующей итерационной формулы … ОТВЕТ: 1 |
1.
|
Математический аппарат и численные методы компьютерного моделирования |
2.
|
||
3.
|
||
4. Итерация Гаусса-Зейделя используется для решения систем … ОТВЕТ: 3 |
1. Нелинейных дифференциальных уравнений в частных производных |
Математический аппарат и численные методы компьютерного моделирования |
2. Нелинейных алгебраических уравнений |
||
3. Линейных алгебраических уравнений |
||
5. Итерация Якоби используется для решения систем … ОТВЕТ: 3 |
1. Нелинейных дифференциальных уравнений в частных производных |
Математический аппарат и численные методы компьютерного моделирования |
2. Нелинейных алгебраических уравнений |
||
3. Линейных алгебраических уравнений |
||
6. Итерация неподвижной точки используется для решения систем … ОТВЕТ: 2 |
1. Нелинейных дифференциальных уравнений в частных производных |
Математический аппарат и численные методы компьютерного моделирования |
2. Нелинейных алгебраических уравнений |
||
3. Линейных алгебраических уравнений |
||
7. Метод Ньютона-Рафсона используется для решения систем … ОТВЕТ: 2 |
1. Линейных дифференциальных уравнений в частных производных |
Математический аппарат и численные методы компьютерного моделирования |
2. Нелинейных алгебраических уравнений |
||
3. Линейных алгебраических уравнений |
||
8. Неравномерной называется сетка, у которой … ОТВЕТ: 3 |
1. Все шаги равны |
Математический аппарат и численные методы компьютерного моделирования |
2. Все шаги не равны друг другу |
||
3. Хотя бы один шаг отличается от остальных |
||
9. В результате дискретизации дифференциальное уравнение в частных производных преобразуется в … ОТВЕТ: 2 |
1. Обыкновенное дифференциальное уравнение |
Математический аппарат и численные методы компьютерного моделирования |
2. Систему алгебраических уравнений |
||
3. Матрицу чисел |
||
10. Какое минимальное число шагов сетки должен иметь шаблон для дискретизации производной второго порядка ОТВЕТ: 2 |
1. Один |
Математический аппарат и численные методы компьютерного моделирования |
2. Два |
||
3. Три |
Тесты для проверки индикатора ПК-1.3 «Владеет математическим аппаратом и методами компьютерных технологий для моделирования объектов нанотехнологии и микросистемной техники».
Вопрос |
Варианты ответа |
Проверяемые знания |
1. Какое из уравнений не входит в фундаментальную систему уравнений полупроводника? ОТВЕТ: 1 |
1. Уравнение диффузии |
Математический аппарат и численные методы компьютерного моделирования |
2. Уравнение непрерывности для электронов |
||
3. Уравнение Пуассона |
||
2. Сколько дифференциальных уравнений в частных производных входит в фундаментальную систему уравнений в гидроднамическом приближении? ОТВЕТ: 3 |
1. Три |
Математический аппарат и численные методы компьютерного моделирования |
2. Пять |
||
3. Семь |
||
3. Сколько дифференциальных уравнений в частных производных входит в фундаментальную систему уравнений в квазигидроднамическом приближении? ОТВЕТ: 2 |
1. Три |
Математический аппарат и численные методы компьютерного моделирования |
2. Пять |
||
3. Семь |
||
4. Сколько дифференциальных уравнений в частных производных входит в фундаментальную систему уравнений в диффузионно-дрейфовом приближении? ОТВЕТ: 1 |
1. Три |
Математический аппарат и численные методы компьютерного моделирования |
2. Пять |
||
3. Семь |
||
5. Сколько вершин имеет шаблон для смешанной производной второго порядка? ОТВЕТ: 3 |
1. Три |
Математический аппарат и численные методы компьютерного моделирования |
2. Четыре |
||
3. Пять |
||
6. Задача о стационарном распределении температуры описывается … ОТВЕТ: 2 |
1. Уравнением непрерывности |
Математический аппарат и численные методы компьютерного моделирования |
2. Уравнением Пуассона |
||
3. Уравнением диффузии |
||
7. Задача о нестационарном распределении концентрации электронов или дырок в полупроводнике описывается… ОТВЕТ: 1 |
1. Уравнением непрерывности |
Математический аппарат и численные методы компьютерного моделирования |
2. Уравнением Пуассона |
||
3. Уравнением Лапласа |
||
8. Оператор носит название … ОТВЕТ: 3 |
1. Оператор набла |
Математический аппарат и численные методы компьютерного моделирования |
2. Оператор Лапласа |
||
3. Оператор Гамильтона |
||
9. Оператор носит название … ОТВЕТ: 1 |
1. Оператор набла |
Математический аппарат и численные методы компьютерного моделирования |
2. Оператор Лапласа |
||
3. Оператор Гамильтона |
||
10. Оператор определяется выражением ОТВЕТ: 2 |
1.
|
Математический аппарат и численные методы компьютерного моделирования |
2.
|
||
3. ни одним из перечисленных |
Вопросы для проверки степени сформированности компетенции «Готов рассчитывать и проектировать компоненты нано- и микросистемной техники (ПК-4)».
1. Запишите результат дискретизации производной первого порядка функции f(x,y,t) в виде правой конечной разности.
2. Запишите результат дискретизации производной первого порядка функции f(x,y,t) в виде левой конечной разности.
3. Запишите результат дискретизации производной первого порядка функции f(x,y,t) в виде центральной конечной разности.
4. Запишите результат дискретизации производной второго порядка функции f(x,y,t).
5. Опишите, чем отличаются явная и неявная схемы численного решения уравнения теплопроводности.
6. Какая последовательность приближений к решению нелинейной системы уравнений называется сходящейся?
7. Какая последовательность приближений к решению нелинейной системы уравнений называется расходящейся?
8. Что называется невязкой?
9. Опишите итерацию Якоби. Для решения каких систем она применяется?
10. Опишите итерацию Гаусса-Зейделя. Для решения каких систем она применяется?
11. Опишите метод Ньютона-Рафсона. Для решения каких систем он применяется?
12. Какая матрица коэффициентов СЛАУ называется строго диагонально доминирующей?
13. Сформулируйте критерий сходимости итераций Якоби и Гаусса-Зейделя.
14. Сформулируйте критерий сходимости итерации неподвижной точки.
15. Сформулируйте критерий сходимости метода Ньютона-Рафсона.
Тесты для проверки индикатора ПК-4.1 «Знает принципы конструирования отдельных блоков компонентов нано- и микросистемной техники».
Вопрос |
Варианты ответа |
Проверяемые знания |
1. Какие физические процессы описывает уравнение Пуассона? ОТВЕТ: 1 |
1. Стационарные |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Нестационарные |
||
3. Стационарные и нестационарные |
||
2. Какая зависимость является решением уравнения теплопроводности? ОТВЕТ: 3 |
1. Зависимость плотности мощности источников тепла от координат |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Зависимость плотности мощности источников тепла от температуры |
||
3. Зависимость температуры от координат и времени |
||
3. Какая зависимость является решением уравнения диффузии? ОТВЕТ: 2 |
1. Зависимость плотности потока частиц от координат |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Зависимость концентрации частиц от координат и времени |
||
3. Зависимость плотности потока частиц от времени |
||
4. Какое из приведенных уравнений описывает незатухающие колебания в однородной среде? ОТВЕТ: 2 |
1.
|
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2.
|
||
3.
|
||
5. Какой оператор обозначается символом ? ОТВЕТ: 1 |
1.
|
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2.
|
||
3.
|
||
6. Как называется
уравнение
|
1. Пуассона |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Теплопроводности |
||
3. Лапласа |
||
7. Что описывают граничные условия Дирихле? ОТВЕТ: 3 |
1. Проекцию градиента искомой физической величины на нормаль к границе |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Скорость изменения искомой физической величины во времени на границе |
||
3. Значения искомой физической величины на границе |
||
8. Что описывают граничные условия Неймана? ОТВЕТ: 1 |
1. Проекцию градиента искомой физической величины на нормаль к границе |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Скорость изменения искомой физической величины во времени на границе |
||
3. Значения искомой физической величины на границе |
||
9. Конвективный отвод тепла от границы моделируемого элемента описывается граничными условиями… ОТВЕТ: 3 |
1. Первого рода |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Второго рода |
||
3. Третьего рода |
||
10. Отвод тепла от границы моделируемого элемента посредством излучения описывается граничными условиями… ОТВЕТ: 3 |
1. Первого рода |
Принципы конструирования отдельных блоков компонентов нано- и микросистемной техники |
2. Второго рода |
||
3. Третьего рода |
Тесты для проверки индикатора ПК-4.2 «Умеет проводить оценочные расчеты характеристик компонентов нано- и микросистемной техники».
Вопрос |
Варианты ответа |
Проверяемые знания |
1. Уравнение
носит название ОТВЕТ: 3 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение теплопроводности |
||
2. Уравнение
носит название ОТВЕТ: 1 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
3. Уравнение
носит название ОТВЕТ: 2 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
4. Уравнение
носит название ОТВЕТ: 2 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
5. Уравнение
носит название ОТВЕТ: 3 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
6. Уравнение
носит название ОТВЕТ: 2 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Волновое уравнение |
||
3. Уравнение непрерывности |
||
7. Уравнение
носит название ОТВЕТ: 2 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Волновое уравнение |
||
3. Уравнение непрерывности |
||
8. Уравнение
носит название ОТВЕТ: 2 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
9. Уравнение
носит название ОТВЕТ: 3 |
1. Уравнение Лапласа |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Уравнение Пуассона |
||
3. Уравнение непрерывности |
||
10. Триангуляцией Делоне называется граф, образованный соединением … ОТВЕТ: 3 |
1. Всех точек координатной сетки отрезками прямых линий |
Оценочные расчеты характеристик компонентов нано- и микросистемной техники |
2. Соседних в смысле Дирихле точек отрезками прямых линий |
||
3. Ближайших точек координатной сетки отрезками прямых линий |

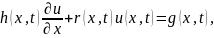
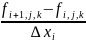
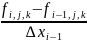
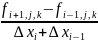
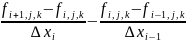
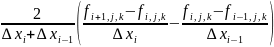
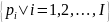 ,
заданной на области ,
множество всех точек ,
расположенных ближе к точке pi,
чем к любой другой точке pj,
называется … ОТВЕТ: 1
,
заданной на области ,
множество всех точек ,
расположенных ближе к точке pi,
чем к любой другой точке pj,
называется … ОТВЕТ: 1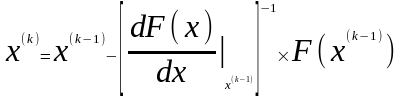
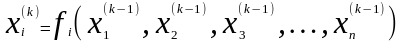
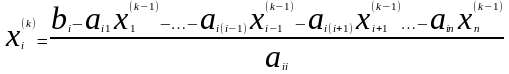
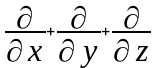
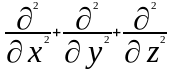
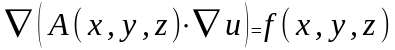

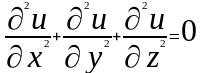
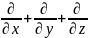
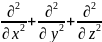
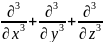
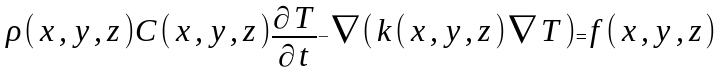 ?
ОТВЕТ: 2
?
ОТВЕТ: 2