Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Омский государственный технический университет» Кафедра” Автоматизация и робототехника”
Отчёт по выполнению домашнего задания
Вариант - 17
Выполнил:
Студент группы АТП-221
Ташбулатов А.
Проверил:
Доц., к.н. Аристов В.В.
Омск 2025
Оглавление
Задание № 1(множества) 3
Задание № 2 (логика Буля) 8
Задание № 3 (Графы) 14
Задание № 4 (Синтез автомата) 16
Задание № 1(множества)
Рисунок 1 – Заданный вариант
Построить диаграмму Эйлера-Венна для операций над тремя множествами, используя следующие выражения
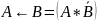
Рисунок
2 – Круги Эйлера для
Рисунок
3 – Круги Эйлера для
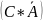
Рисунок 4 – Круги Эйлера для Y
Преобразовать эти логические выражения, используя законы булевой логики, разложить на конституенты нуля и единицы, представить таблицей состояний и матрицей Карно, произвести минимизацию функции и записать ее в виде ДНФ и КНФ
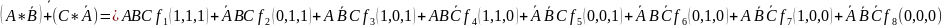
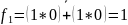
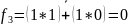
Таблица 1 – Таблица истинности
A |
B |
C |
Y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Таблица 2 – Карта Карно
A/BC |
00 |
01 |
11 |
10 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
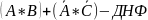
– КНФ
Преобразовать их в базис И, ИЛИ, НЕ с реализацией в виде РКС
Рисунок 5 – Схема РКС, где I1 – A, I2 – B, I3 – C
Преобразовать в базисы И-НЕ и ИЛИ-НЕ с реализацией в виде БЛС. Проверить по таблице состояний все три базиса программой "LOGO Soft Comfort".
Для перевода логического выражения в базис И-НЕ надо в ДНФ охватить скобками все элементарные конъюнкции, и записать выражение такого же вида, в котором все отрицания остаются при тех же аргументах функции, а все знаки & и + заменяются Штрихом Шеффера |. Если какая-то из элементарных конъюнкций представлена в ДНФ всего одной переменной, то при переходе в базис И-НЕ эта переменная инвертируется
Рисунок 6 – Схема БЛС для базиса И-НЕ, где I1 – A, I2 – B, I3 – C
Для
перевода логического выражения в базис
ИЛИ-НЕ надо для КНФ записать выражение
такого же вида, в котором все отрицания
остаются при тех же аргументах функции,
а все знаки & и 
заменяются
стрелкой Пирса ↓.
Если какая-то из
элементарных дизъюнкций представлена
в КНФ всего одной переменной, то при
переходе в базис ИЛИ-НЕ эта переменная
инвертируется
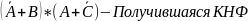
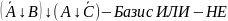
Рисунок 7 – Схема БЛС для базиса ИЛИ-НЕ, где I1 – A, I2 – B, I3 – C
Задание № 2 (логика Буля)
Произведите аналитическим путем преобразования и упрощение (например, приведение к ДНФ или КНФ) левой и правой частей тождества с целью его доказательства.
Рисунок 8 – Индивидуальный вариант
Полученная левая часть
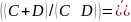
Полученная правая часть
Левая и правая части тождества не равны
По заданным диаграммам Эйлера-Венна представьте логические функции в виде СДНФ и СКНФ.
Рисунок 9 – Индивидуальный вариант
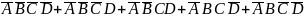– Полученная
функция в виде СДНФ
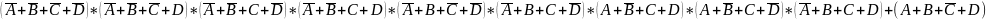– Полученная
функция в виде СКНФ
Составьте для этих функций таблицы истинности и матрицы Карно.
Таблица 3 – Таблица истинности
A |
B |
C |
D |
Y |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Таблица 4 – Карта Карно
AB|CD |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
1 |
0 |
01 |
1 |
0 |
0 |
1 |
11 |
0 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
Произведите минимизацию функций методами Квайна–МакКласски, Гаврилова-Копыленко и по матрицам Карно. Сравните результаты минимизации.
Минимизация Карно:
МДНФ:
МКНФ:
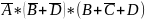
Минимизация функций методом Квайна и Мак-Класки:
Таблица 5
-
Наборы
Десятичный эквивалентный набор переменных
Переменные и их разряды
№ группы
A
B
C
D
Единичные
2
0
0
0
1
1
3
0
0
1
1
2
4
0
1
1
0
2
5
0
1
0
0
1
Таблица 6
-
№
Десятичный эквивалентный набор переменных
Переменные и их разряды
A
B
C
D
1
2
0
0
0
1
✔
5
0
1
0
0
✔
2
4
0
0
1
1
✔
7
0
1
1
0
✔
Таблица 7
-
№
Десятичный эквивалентный набор переменных
Переменные и их разряды
A
B
C
D
1
2-4
0
0
-
1
✔
5-7
0
1
-
0
✔
Таблица 8
Простые импликанты |
Конституенты единиицы |
||||
0000 |
0001 |
0011 |
0110 |
0010 |
|
0000 |
+ |
|
|
|
|
00-1 |
|
+ |
+ |
|
+ |
01-0 |
|
|
|
+ |
+ |
Минимизированная функция:
Вывод: Сравним результаты двух методов матрицы Карно и Квайна и Мак-Класки. Оба метода показали одинаковый результат, что доказывает правильность минимизации.
Произвести минимизацию булевой функции, заданной десятичными номерами состояний по матрицам Карно. Получить минимальные ДНФ (выделяя подкубы по единичным значениям функции) и КНФ (выделяя подкубы по нулевым значениям функции).
Y1 = {7,8,11,13,15,16,2,28,29,31}; YФ ={4,5,9,10,18,20,23,24,26,30}.
Рисунок 10 – Карта Карно
МДНФ:
Рисунок 11 – Схема РКС, где I1 – A, I2 – B, I3 – C, I4 – D, I5 – E
Рисунок 12 – Карта Карно
МКНФ:
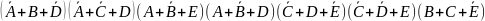
Рисунок 13 – Схема БЛС, где I1 – A, I2 – B, I3 – C, I4 – D, I5 – E