Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Омский государственный технический университет» Кафедра” Автоматизация и робототехника”

Отчёт по выполнению домашнего задания

Вариант - 17

Выполнил:

Студент группы АТП-221

Проверил:

Доц., к.н. Аристов В.В.

Омск 2025

Оглавление

Задание № 3 (Графы) 3

Задание № 4 (Синтез автомата) 5

Задание № 3 (Графы)

Граф задан множеством вершин V и множеством ребер X. Инцидентор графа Р определен истинными значениями, представленными в табл.12. Построить граф, составить матрицы смежности и инцидентности, определить центр графа.

Таблица 1 – Заданный вариант:

№	V = {…}	X = {…}	Инцидентор графа Р
17	a,b,c,d,е,g	1, 2, 3, …, 10	P(a,1,c); P(c,2,g); P(g,3,b); P(е,4,a); P(b,5,e); P(g,6,d); P(b,7,b); P(e,8,e); P(g,9,a); P(c,10,d)

Граф задан множеством вершин V={a,b,c,d,e,f,g } и множеством рёбер X = {1, 2, 3, …, 10}. Инцидентор P определяет связи между вершинами и рёбрами следующим образом:

• P(a,1,с) — ребро 1 соединяет вершины a и с.

• P(с,2,g) — ребро 2 соединяет вершины c и g.

• P(g,3,b) — ребро 3 соединяет вершины g и b.

• P(e,4,a) — ребро 4 соединяет вершины e и a.

• P(b,5,e) — ребро 5 соединяет вершины b и e.

• P(g,6,d) — ребро 6 соединяет вершины g и d.

• P(b,7,b) — ребро 7 соединяет вершины b и b.

• P(e,8,e) — ребро 8 соединяет вершины e и e.

• P(g,9,a) — ребро 9 соединяет вершины g и a.

• P(c,10,d) — ребро 10 соединяет вершины c и d.

Рисунок 1 – Построенный граф P

Матрица инцидентности

Матрица инцидентности B размером 6×10 (вершины × рёбра) отражает инцидентность вершин и рёбер. Элемент B_ij равен:

• 1, если ребро j выходит из вершины i,

• -1, если ребро j входит в вершину i,

• 0 в остальных случаях.

Матрица смежности

Матрица смежности AA размером 7×7 (по количеству вершин) отражает наличие рёбер между вершинами. Элемент Aij​ равен 1, если есть ребро из вершины i в вершину j, и 0 в противном случае.

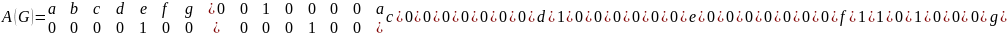
Для определения центра графа необходимо рассчитать путь при переходе к одной вершины из каждой остальной. При этом для каждой вершины выбрать наибольшее и определить наименьшее значение из наибольших, так как оно будет являться центром графа.

Таблица 2 – Таблица путей между вершинами

В Из	a	b	c	d	e	f	g
a	-	3	1	2	4	-	2
b	2	-	3	4	1	-	4
c	2	2	-	1	3	-	1
d	-	-	-	-	-	-	-
e	1	4	2	3	-	-	3
f	-	-	-	-	-	-	-
g	1	1	2	1	2	-	-

Сравним максимальные значения из каждого столбца и получим, что g являются центрами графа.

Задание № 4 (Синтез автомата)

Таблица 3 – Индивидуальный вариант

Вариант задания	Алгоритм работы	Механизмы
		A	B	C
15	C – B – nC – nB – A – nA	9	10	1

Рисунок 2 – Механизм А

Рисунок 3 – Механизм Б

Рисунок 4 – Механизм С

В соответствии вариантом алгоритма работы механизмов произвести анализ работы автоматической установки в виде словесного описания, построить циклограмму работы, граф функционирования и граф переходов.

Рисунок 5 – Граф функционирования

Рисунок 6 – Циклограмма работы

Рисунок 7 – Граф переходов

Произведём синтез дискретной системы управления блочным методом

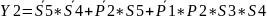
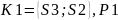
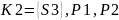
По полученным в результате синтеза логическим уравнениям построить принципиальные релейно-контактную (РКС) и бесконтактную логическую схемы (БЛС).

Рисунок 8 – Схема РКС

Рисунок 9 – Схема БЛС

Проверить работу спроектированной системы управления программой «Logo Soft Comfort»

Рисунок 10 – Программная реализация с использованием программы «LOGO Soft Comfort»