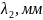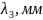ЭД 1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №1

по дисциплине «Электродинамика»

Тема: ИССЛЕДОВАНИЕ ДИСПЕРСИИ ВОЛН

В ВОЛНОВОДЕ И В КОАКСИАЛЬНОЙ ЛИНИИ ПЕРЕДАЧИ

Студенты гр. 2281		Зимин И.П.
Преподаватель		Дроздовский А.В.

Санкт-Петербург

2024

Цель работы.

Изучение дисперсионных свойств волн, распространяющихся в коаксиальной линии и прямоугольном волноводе, а также методики измерения длины волны в линии передачи и параметров, характеризующих режим ее работы; приобретение практических навыков работы с векторным анализатором цепей для измерения передаточных характеристик и закона дисперсии.

Основные теоретические положения

СВЧ-линией передачи называется устройство, ограничивающее область распространения электромагнитных волн СВЧ-диапазона и позволяющее передавать поток их электромагнитной энергии в заданном направлении

Электромагнитные волны, распространяющиеся в линии передачи, делятся на:

– электрические волны (Е-, ТМ-волны), вектор напряженности электрического поля которых имеет как поперечные, так и продольную составляющие, а вектор напряженности магнитного поля – только поперечные;

– магнитные волны (H-, ТЕ-волны), вектор напряженности магнитного поля которых имеет как поперечные, так и продольную составляющие, а вектор напряженности электрического поля – только поперечные;

– поперечные электромагнитные волны (ТЕМ-волны), векторы напряженности электрического и магнитного полей которых лежат в плоскости, перпендикулярной направлению распространения.

Длина волны в линии передачи определяется следующим соотношением:

Закон дисперсии волноведущей структуры:

Коаксиальная линия передач является двухсвязной линией передач и в ней наряду с E и H волнами возможно распространение TEM волны, которая является волной основного типа для коаксиальной линии. TEM волная является волной бездисперсионного типа, для которой , .

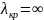В прямоугольном волноводе могут распространятся только волны дисперсионного типа и . Критическая длина волны определяется как

Описание установки

Блок-схема установки для измерения длины волны в линии передач (рис.1). Коаксиальная измерительная линия - цилиндрический проводник между плоскопараллельными наружными пластинами. Такая линия бездисперсионная и структура поля в ней близка к коаксиальной линии.

Рис. 1 Блок схема измерительной установки

Измерительная схема, используемая для исследования ФЧХ при помощи анализатора цепей, представлена на рис. 2.

Рис. 2 Измерительная схема для исследования ФЧХ при помощи ВАЦ

Обработка результатов измерений

1. Коаксиальный кабель

Рассчитаем длины волн 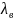и волновые числа в коаксиальной линии передач с помощью экспериментально полученных распределений минимумов стоячей волны при разных частотах генератора (таблица 1). Также рассчитаем их теоретические значения, учитывая, что для коаксиальной ЛП . Результаты расчетов занесем в таблицу 2.

Таблица 1

Распределение минимумов волны в коаксиальной ЛП

3365	73	116	161	206
3425	79	125	169	208
3540	57,6	100	142,5	185
3688	80	125	157	201
3815	60	96	140	178
3925	75	114	152	187

Пример расчета для :

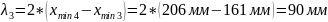
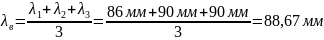
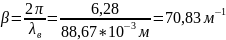
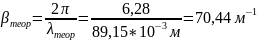
Таблица 2

Экспериментальные и теоретические значения для коаксиальной ЛП

3365	86	90	90	88,67	70,83	89,15	70,44
3425	92	88	78	86,00	73,02	87,59	71,70
3540	84,8	85	85	84,93	73,94	84,75	74,10
3688	90	64	88	80,67	77,85	81,34	77,20
3815	72	88	76	78,67	79,83	78,64	79,86
3925	78	76	70	74,67	84,11	76,43	82,16

По полученным значения построим экспериментальные и теоретические зависимости и 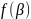(рис.3 и рис.4).

Рис. 3 Экспериментальная и теоретическая зависимость длины волны от частоты для коаксиальной ЛП

Рис. 4 Экспериментальный и теоретический закон дисперсии коаксиальной ЛП

С помощью ФЧХ определим экспериментальный закон дисперсии для коаксиальной линии передач , где – набег фазы в ЛП, – длина ЛП. Изобразим на одном графике экспериментальный и теоретический законы дисперсии (рис. 5).

Рис. 5 Теоретический и экспериментальный законы дисперсии из ФЧХ

2. Прямоугольный волновод

Экспериментально определим частоту отсечки по зависимости коэффициента передачи (рис. 6)

Рис. 6 Частотная зависимость для прямоугольного волновода

Рассчитаем теоретическую частоту отсечки основной моды , исходя из геометрических размеров волновода.

Изобразим на графике экспериментальный закон дисперсии волновода, полученный на основе измерения фазового набега и теоретический (рис.7).

Рис. 7 Экспериментальный и теоретический законы дисперсии для прямоугольного волновода

Вывод: в ходе выполнения лабораторной работы были изучены дисперсионные свойства волн, распространяющихся в коаксиальной линии и прямоугольном волноводе.

По построенной экспериментальной зависимости длины волны в коаксиальной линии от частоты видно, что с ростом частоты длина волны в коаксиальной линии уменьшается, что совпадает с теоретическими расчетами.

Полученный закон дисперсии для коаксиальной линии имеет линейных характер, что согласуется с теорией и подтверждает бездисперсионность TEM – волны, которая является волной основного типа для данной линии передачи.

Для прямоугольного волновода определена частота отсечки двумя способами: через экспериментальный график коэффициента передачи ( ) и с помощью расчета через геометрические размеры волновода для основной моды ( .

Также были построены расчетный теоретический закон дисперсии и экспериментальный закон дисперсии, полученный на основе измерения набега фазы. На полученных зависимостях видно отклонение от линейного закона, что подтверждает дисперсионность волновода.