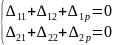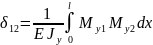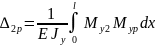МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ПМИГ

отчет

по индивидуальному домашнему заданию № 2.2

по дисциплине «Прикладная механика»

Тема: Решение статически неопределимой задачи графическим методом

Студент гр. 2281		Зимин И.П.
Преподаватель		Титов А.В.

Санкт-Петербург

2025

Содержание

1 Задание и исходные данные 3

2 Раскрытие статической неопределимости 4

1 Задание и исходные данные

Тема: Решение статически неопределимой задачи аналитическим методом.

Дано: расчетная схема (см. Приложение А)

Требуется:

1. Раскрыть статическую неопределимость

Рисунок 1 – Исходная схема

2 Раскрытие статической неопределимости

Обозначим направление осей и реакции в опорах на рисунке 2.

Рисунок 2 – Направление осей и реакций в опорах

Раскроем неопределимость графическим методом, для этого отбросим лишнюю заделку и заменим силами 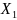и . (рисунок 3).

Рисунок 3 – Решение неопределимости методом сил

Составим систему уравнений (1) и (2).

(1)

(2)

Подставим (2) в (1) и получим систему (3).

(3)

Для определения перемещений от единичных сил воспользуемся интегралами Мора (4) - (9).

	(4)
	(5)
	(6)
	(7)
	(8)
	(9)

Для нахождения перемещений воспользуемся правилом Верещагина. Первоначально определим моменты, создаваемые единичными силами.

Определим . Убираем всё кроме (рисунок 4).

Рисунок 4 – Определение

Определим внутренний момент по методу сечений (рисунок 5)

Рисунок 5 – Решение методом сечений

Определим 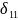графическим методом. Построим эпюру (рисунок 6).

Рисунок 6 – Эпюра

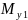
Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

Определим . Для этого убираем всё кроме (рисунок 7).

Рисунок 7 – Определение

Определим внутренний момент по методу сечений (рисунок 8).

Рисунок 8 – Решение методом сечений

Определим графическим методом. Построим эпюру и (рисунок 9).

Рисунок 9 – Эпюра и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

Определим графическим методом, перемножив эпюры в другом порядке. Построим эпюру и (рисунок 10).

Рисунок 10 - Эпюра и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

Определим графическим методом. Построим эпюру (рисунок 11).

Рисунок 11 – Эпюра

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

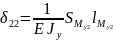
Определим . Уберем всё кроме P (рисунок 12).

Рисунок 12 – Определение

Определим внутренний момент по методу сечений (рисунок 13).

Рисунок 13 – Решение методом сечений

Определим графическим методом. Построим эпюру и 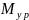(рисунок 14).

Рисунок 14 – Эпюра и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

Определим графическим методом, перемножив эпюры в другом порядке. Построим эпюры и (рисунок 15 )

Рисунок 15 – Эпюры и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

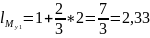
Определим графическим методом. Построим эпюры и (рисунок 16)

Рисунок 16 – Эпюры и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

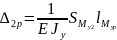
Определим графическим методом, перемножив эпюры в другом порядке.Построим эпюры и (рисунок 17).

Рисунок 17 – Эпюры и

Найдем площадь эпюры :

Найдем ординату другой эпюры, расположенной под центром тяжести первой эпюры:

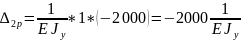
Подставим найденные перемещения в (3) и решим полученную систему: