
Лабораторные работы / Лабораторная работа №4 (16)
.docxМинистерство цифрового развития, связи и массовых
коммуникаций Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра «Теория электрических цепей»
Лабораторная работа №4
«Исследование на ЭВМ резонансных явлений в пассивном последовательном колебательном контуре (без гиратора)»
Выполнил студент группы
------
Проверил доцент кафедры «Теория электрических цепей»
-------
Москва 2025
Задание
1.1 Рассчитать величину индуктивности L, выбрав из заданного интервала величину ёмкости C ∈ [10; 40] нФ так, чтобы резонансная частота пассивного последовательного колебательного контура (рис. 1) составила f0 = 5 кГц.

Рисунок 1 – Последовательный колебательный контур.
1.2 Рассчитать следующие параметры последовательного контура (U1 = 1 В):
ρ — характеристическое сопротивление;
Q — добротность;
f1 — нижнюю граничную частоту;
f2 — верхнюю граничную частоту;
П — абсолютную полосу пропускания;
I0 — модуль входного тока при резонансе.
Расчеты провести для двух значений сопротивления R = 160 и 640 Ом.
Таблица 1
По предварительному расчету U1=1 В, f0=5 кГц, C=10нФ , L=0,101Гн |
Получено эксперементально |
|||||||||||||||||||||||
|
|
|
|
|
|
мА
|
|
Гц
|
мА
|
|
|
|
|
|
||||||||||
160 |
3178 |
19,86 |
4875,7 |
5127,4 |
251,73 |
6,25 |
5 |
5007 |
6.249 |
4883 |
5136 |
253 |
19,7 |
|
||||||||||
640 |
3178 |
4,97 |
4521,8 |
5528,7 |
1006,9 |
1,563 |
5 |
5007 |
1.562 |
4529 |
5537 |
1008 |
4,98 |
|
||||||||||
1.3 На одном графике построить три зависимости входного сопротивления от частоты f ∈ [2; 8] кГц, R = 160 Ом и R=640 Ом:
• модуля входного сопротивления |ZBX(f)|;
• действительной части входного сопротивления Re[ZBX(f)];
• мнимой части входного сопротивления Im[ZBX(f)].

Рисунок 2 – Графики зависимости модуля входного сопротивления (синий), действительной части входного сопротивления (красный), мнимой части входного сопротивления (зеленый) от частоты при R=160 Ом.

Рисунок 3 – Графики зависимости модуля входного сопротивления (синий), действительной части входного сопротивления (красный), мнимой части входного сопротивления (зеленый) от частоты при R=640 Ом.
1.4 Построить на одном графике зависимости фазы входного сопротивления φZвх(f) = arg[ZBX(f)] от частоты f ∈ [2; 8] кГц для двух значений сопротивления R = 160 и 640 Ом.

Рисунок 3 – Графики зависимости фазы входного сопротивления от частоты.
1.5 Построить на одном графике резонансные кривые, т.е. зависимости модуля входного тока |I(f)| последовательного контура от частоты f ∈ [2; 8] кГц для двух значений сопротивления R=160 и 640 Ом.

Рисунок 4 – Графики зависимости модуля входного тока от частоты.

Рисунок 6 – График модуля входного тока R=160 Ом

Рисунок 6 – График модуля входного тока для R=640 Ом
Контрольные вопросы
1. Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?
Резонанс в последовательном колебательном контуре называется резонансом напряжений, потому что при этом явлении напряжение на катушке равняется напряжению на конденсаторе.
2. Как рассчитывается резонансная частота сложного пассивного колебательного контура?
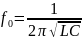
3. Что такое добротность последовательного пассивного колебательного контура?
Добротность последовательного пассивного колебательного контура — величина, которая определяет амплитуду и ширину АЧХ резонанса. Она показывает, во сколько раз сохранённой энергии в колебательном контуре больше, чем потери энергии за единичный период колебаний.
4. Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?
Полосой
пропускания контура
– это полоса частот, в пределах которой
ток в контуре уменьшается не более чем
в
 раз
по сравнению с током при резонансе.
раз
по сравнению с током при резонансе.
Способы расчета полосы пропускания:
5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.
Входная АЧХ определяется выражением:

Входная ФЧХ определяется выражением:





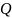
 Гц
Гц Гц
Гц

 кГц
кГц


