Лабораторные работы. Владимиров / Оптимизация_Практика_9_Отчет_(Границы)

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА»

Факультет инфокоммуникационных сетей и систем

Кафедра вычислительной техники и программной инженерии

ПРАКТИЧЕСКАЯ РАБОТА №9

По дисциплине

«Оптимизация и математические методы принятия решений»

Вариант 22

Выполнил:

Студент 2-го курса

Дневного отделения

Группы ИКПИ-32

Андреев А. А.,

Жилкин Д. А,

Яковлев М. А.

Преподаватель:

Владимиров С. А.

Санкт-Петербург

2025

Цель работы

Выполнить постановку и нахождение оптимального решения в нелинейных задачах, записанных в виде аналитических функций, используя метод множителей Лагранжа и теорему Каруша-Куна-Таккера.

Постановка задачи

Найти решение для следующей задачи:

Ход работы

1. Определение типа задачи.

Составим матрицу вторых производных целевой функции f(x):

Главные миноры этой матрицы:

Главные миноры неотрицательные. Таким образом, целевая функция является выпуклой. Ограничения задачи линейны. Следовательно, исходная задача является задачей выпуклого программирования.

2. Введем множество 𝑄 = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ ≥ 0, 𝑥 ∈ 𝑅³ }. Запишем задачу в виде

𝑓(𝑥) = 𝑥₁² + 𝑥₂² + 𝑥₃² → 𝑚𝑖𝑛

Ограничения задачи выражены в виде линейных функций, значит, проверка условия Слейтера не требуется.

3. Составим функцию Лагранжа:

𝐹(𝑥, 𝜆) = 𝑥₁² + 𝑥₂² + 𝑥₃² + 𝜆₁(2𝑥₁ − 𝑥₂ + 4𝑥₃ − 1) + 𝜆₂(𝑥₁ − 𝑥₃ − 3),

𝑥 ∈ 𝑄, 𝜆 ∈ 𝑅², 𝜆₂

Найдем стационарные точки функции Лагранжа:

Решив данную систему методом Гаусса, получим: x₁ = 0.61, x₂ = 0.84, x₃ = 0.15, 𝜆₁ = −0.28, 𝜆₂ = −0.65, что противоречит условию. Стационарных точек нет. Будем проверять наличие решения на границах множества 𝑄:

• 𝐿₁ = {𝑥: 𝑥₁ = 0, 𝑥₂ ≥ 0, 𝑥₃ ≥ 0}

• 𝐿₂ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ = 0, 𝑥₃ ≥ 0}

• 𝐿₃ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ ≥ 0, 𝑥₃ = 0}

• 𝐿₄ = {𝑥: 𝑥₁ = 0, 𝑥₂ = 0, 𝑥₃ ≥ 0}

• 𝐿₅ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ = 0, 𝑥₃ = 0}

• 𝐿₆ = {𝑥: 𝑥₁ = 0, 𝑥₂ ≥ 0, 𝑥₃ = 0}

• 𝐿₇ = {𝑥: 𝑥₁ = 𝑥₂ = 𝑥₃ = 0}

4. Рассмотрим 𝐿₁ = {𝑥: 𝑥₂ ≥ 0, 𝑥₁ = 0, 𝑥₃ ≥ 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₂² + 𝑥₃² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₁:

𝐹(𝑥, 𝜆) = 𝑥₂² + 𝑥₃² + 𝜆₁(−𝑥₂ + 4𝑥₃ − 1) + 𝜆₂(3𝑥₂ – 𝑥₃ − 3), 𝑥₂ ≥ 0, 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Получим x₁ = 0, x₂ = 1.1, x₃ = 0.54, 𝜆₁ = −0.951 𝜆₂ = −0.95, что противоречит условию 𝜆₂ ≥ 0.

5. Рассмотрим 𝐿₂ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ = 0, 𝑥₃ ≥ 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₁² + 𝑥₃² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₂:

𝐹(𝑥, 𝜆) = 𝑥₁² + 𝑥₃² + 𝜆₁(2𝑥₁ + 4𝑥₃ − 1) + 𝜆₂(𝑥₁ − 𝑥₃ − 3), 𝑥_1,3 ≥ 0, 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Из решения методом Гаусса, получим:

𝜆₁ = ; 𝜆₂ = ; ;

Так как 𝜆₂ ≥ 0, то решение не подходит.

6. Рассмотрим 𝐿₃ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ ≥ 0, 𝑥₃ = 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₁² + 𝑥₂² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₃:

𝐹(𝑥, 𝜆) = 𝑥₁² + 𝑥₂² + 𝜆₁(2𝑥₁ + 𝑥₂ − 1) + 𝜆₂(𝑥₁ + 3𝑥₂ − 3), 𝑥_1,2 ≥ 0, 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Из решения методом Гаусса, получим:

𝜆₁ = ; 𝜆₂ = ; ;

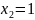
Так как 𝜆₂ ≥ 0, то решение не подходит.

7. Рассмотрим 𝐿₄ = {𝑥: 𝑥₁ = 0, 𝑥₂ = 0, 𝑥₃ ≥ 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₃² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₄:

𝐹(𝑥, 𝜆) = 𝑥₃² + 𝜆₁(4𝑥₃ − 1) + 𝜆₂(𝑥₃ − 3), 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Из решения этой системы методом Гаусса, получим, что нет решений.

8. Рассмотрим 𝐿₅ = {𝑥: 𝑥₁ ≥ 0, 𝑥₂ = 0, 𝑥₃ = 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₁² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₅:

𝐹(𝑥, 𝜆) = 𝑥₁² + 𝜆₁(2𝑥₁ − 1) + 𝜆₂(𝑥₁ − 3), 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Система решений не имеет.

9. Рассмотрим 𝐿₆ = {𝑥: 𝑥₁ = 0, 𝑥₂ ≥ 0, 𝑥₃ = 0}.

Задача примет вид 𝑓(𝑥) = 𝑥₂² → 𝑚𝑖𝑛

Запишем функцию Лагранжа для задачи на границе 𝐿₆:

𝐹(𝑥, 𝜆) = 𝑥₂² + 𝜆₁(−𝑥₂ − 1) + 𝜆₂(3𝑥₂ − 3), 𝜆₂ ≥ 0

Составим систему для нахождения стационарных точек:

Условия и противоречивы, система не имеет решений.

10. Рассмотрим 𝐿₇ = {𝑥: 𝑥₁ = 0, 𝑥₂ = 0, 𝑥₃ = 0}.

Решение не может быть найдено.

11. Заключение.

Оптимального решения не найдено.

Программа

#include <iostream>

#include <vector>

#include <cmath>

using namespace std;

int main() {

// Создаем матрицу коэффициентов

vector<vector<double>> matrix = {

{2, 0, 0, 2, 1, 0},

{0, 2, 0, -1, 3, 0},

{0, 0, 2, 4, -1, 0},

{2, -1, 4, 0, 0, 1},

{1, 3, -1, 0, 0, 3}

};

int n = matrix.size();

// Прямой ход метода Гаусса

for (int i = 0; i < n; i++) {

// Поиск максимального элемента в столбце

int maxRow = i;

for (int k = i + 1; k < n; k++) {

if (abs(matrix[k][i]) > abs(matrix[maxRow][i])) {

maxRow = k;

}

}

// Обмен строк

if (maxRow != i) {

swap(matrix[i], matrix[maxRow]);

}

// Приведение к треугольному виду

for (int k = i + 1; k < n; k++) {

double factor = matrix[k][i] / matrix[i][i];

for (int j = i; j <= n; j++) {

matrix[k][j] -= factor * matrix[i][j];

}

}

}

// Обратный ход

vector<double> solution(n);

for (int i = n - 1; i >= 0; i--) {

solution[i] = matrix[i][n];

for (int j = i + 1; j < n; j++) {

solution[i] -= matrix[i][j] * solution[j];

}

solution[i] /= matrix[i][i];

}

cout << "Решение системы:" << endl;

cout << "x = " << solution[0] << endl;

cout << "y = " << solution[1] << endl;

cout << "z = " << solution[2] << endl;

cout << "a = " << solution[3] << endl;

cout << "b = " << solution[4] << endl;

return 0;

}