Реферат_Исуп

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ.ПРОФ.М.А.БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет: «Институт магистратуры»

Кафедра: «Систем автоматизации и робототехники»

Направление подготовки:	Автоматизация технологических процессов и производств
Направленность (профиль):	Интеллектуальные технологии в автоматизации

Реферат

по дисциплине:

Интеллектуальные системы управления производственными процессами

на тему:

Модель исследования динамики высыхания мазута на горизонтальной поверхности бетона

		Выполнил студент группы:
дата, подпись		Фамилия И. О. Принял к.т.н., доцент
		Макаров Л.М.
дата, подпись		Фамилия И. О.

Санкт-Петербург

2025

ОГЛАВЛЕНИЕ

1. Модель Oil Surface Flow Screening Model (OILSFSM) 2

Заключение 16

Список литературы 17

Разливы нефтепродуктов на твердых поверхностях представляют серьёзную экологическую и техногенную проблему. При таких авариях жидкость быстро распространяется по поверхности, загрязняя почву и создавая пожароопасные зоны. Поверхностные разливы нефтепродуктов часто происходят при транспортировке, переработке и хранении топлива, они могут уничтожить окружающую почву и представлять угрозу людям и объектам, особенно при воспламенении

Наиболее распространённые модели распространения пятен нефтепродуктов учитывают режим течения «гравитационно-вязкого» (после начального инерционного этапа)

При этом важную роль играют вязкость жидкости, поверхностное натяжение, а также поглощение и испарение. Например, модель OILSFSM специально учитывает инфильтрацию в пористое основание (модель Грина–Ампта) и испарение на поверхности

Понимание того, как различные виды горючих жидкостей распространяются по различным поверхностям при случайном разливе, имеет решающее значение для предотвращения эскалации аварий, связанных с такими проливами. Огромные объёмы горючих жидкостей — бензин, дизельное топливо, керосин, сжиженный нефтяной газ (СПГ) и сжатый природный газ (СПГ) — производятся, заправляются, хранятся, транспортируются и используются круглосуточно по всему миру, что постоянно поддерживает высокий риск случайной утечки. Масштаб этой угрозы можно оценить по тому факту, что большинство крупных промышленных катастроф, унесших жизни и причинивших сотни миллиардов долларов убытков, начались именно с простого разлива. Во многих случаях проливы становились причиной крупных пожаров и взрывов, превращая первоначально небольшую аварию в ужасную трагедию. В данной работе представлен современный обзор моделей, разработанных для прогнозирования динамики разлива горючих жидкостей.

Модели разлива описывают процессы распространения, испарения и образования луж жидкости на различных типах поверхностей. Степень опасности, связанная с аварийным разливом горючего или токсичного вещества, зависит от интенсивности источника паров, размера лужи и временного поведения разлитой жидкости. Эти параметры можно предсказать с помощью моделей, разработанных для оценки объёма разлива, скорости испарения жидкости и других аспектов поведения разлива. Ниже приведён обзор моделей разлива жидкостей на суше.

1. Модель Oil Surface Flow Screening Model (OILSFSM)

Oil Surface Flow Screening Model (OILSFSM) — это скрининговая модель, предназначенная для прогнозирования поверхностного разлива нефти с учётом процессов инфильтрации в почву и испарения. Она состоит из трёх взаимосвязанных модулей: модуля поверхностного стока, модуля инфильтрации (на основе модели Грина–Ампта) и модуля испарения. Модель применима как для горизонтальных, так и наклонных проницаемых поверхностей, и позволяет моделировать как мгновенные, так и непрерывные точечные разливы чистых жидкостей. [1]

Модуль поверхностного стока может рассчитываться, как и для горизонтальной поверхности (1):

Где:

Veff​(t) — текущий объём жидкости на поверхности в момент времени t, м³.,

V(t) — общий объём разлитой жидкости к моменту времени t, м³.,

t — время с момента начала разлива, с.,

m — показатель, зависящий от геометрии распространения (например, m=1 для линейного источника, m=2 для точечного источника).,

x — координата вдоль направления распространения разлива, м.,

x_N(t) — протяжённость разлива в момент времени t, м. рассчитывается по формуле (2),

q_i(x,t) — поток инфильтрации в точке x и момент времени t, м/с.,

q_e(x,t) — поток испарения в точке x и момент времени t, м/с.,

h_d — глубина затопления (толщина слоя жидкости), м.

Так и для наклонной поверхности (2):

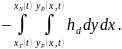
Где:

Veff​(t) — текущий объём жидкости на поверхности в момент времени t, м³.,

V(t) — общий объём разлитой жидкости к моменту времени t, м³.,

t — время с момента начала разлива, с.,

x — координата вдоль направления распространения разлива, м.,

x_N(t) — протяжённость разлива в момент времени t, м. рассчитывается по формуле (2),

x_T​(t) — начальная координата распространения разлива вдоль наклона в момент времени t, м.,

y_P(x,t) — граница распространения разлива в поперечном направлении в точке x и момент времени t, м.,

q_i(x,t) — поток инфильтрации в точке x и момент времени t, м/с.,

q_e(x,t) — поток испарения в точке x и момент времени t, м/с.,

h_d — глубина затопления (толщина слоя жидкости), м.

Протяжённость разлива x_N(t) для горизонтальной поверхности определяется как:

Где:

x_N​(t) — протяжённость разлива в момент времени t, м.,

ξ_N ​ — безразмерная константа, зависящая от типа разлива и источника,

R — коэффициент, учитывающий свойства жидкости и поверхности,

V — объём разлитой жидкости, м³.,

t — время с момента начала разлива, с.,

m — показатель, зависящий от геометрии распространения разлива.

Скорость распространения фронта разлива рассчитывается следующим образом:

Где: 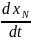— скорость распространения фронта разлива в момент времени t, м/с.,

α — безразмерный коэффициент, зависящий от условий разлива,

m — показатель, зависящий от геометрии распространения разлива,

R — коэффициент, учитывающий свойства жидкости и поверхности,

ξ_N ​ — безразмерная константа, зависящая от типа разлива и источника,

t — время с момента начала разлива, с.,

V_eff — эффективный объём жидкости на поверхности, м³.

Минимальная толщина плёнки находится так:

Где:

h_min​ — минимальная толщина плёнки разлитой жидкости, м.,

h_s​ — начальная толщина плёнки, м.,

h_d — глубина затопления, м.

Данная скрининговая модель может учитывать, как линейные, так и точечные источники. Для линейного источника выполняется условие сохранения объёма в проекции и рассчитывается следующим образом (5):

Где:

x — координата в направлении уклона.

h(x,t) — толщина слоя жидкости в точке x в момент времени t, м.,

x_N​(t) — протяжённость разлива в момент времени t, м.,

x_T​(t) — начальная координата распространения разлива вдоль наклона в момент времени t, м.,

V(t) — общий объём разлитой жидкости к моменту времени t, м³.

Для точечного источника используется выражение (6):

Где:

y_P​(x,t) — полуширина разлива в поперечном направлении в точке x в момент времени t, м.,

y — координата в поперечном направлении уклона,

x — координата в направлении уклона,

h(x,t) — толщина слоя жидкости в точке x в момент времени t, м.,

x_N​(t) — протяжённость разлива в момент времени t, м.,

x_T​(t) — начальная координата распространения разлива вдоль наклона в момент времени t, м.,

V(t) — общий объём разлитой жидкости к моменту времени t, м³.

Протяжённость разлива x_N(t) для наклонной поверхности при линейном источнике определяется как:

Где: x_N​(t) — протяжённость разлива в момент времени t, м.,

ξ_N ​ — безразмерная константа, зависящая от типа разлива и источника,

V — объём разлитой жидкости, м³.,

θ — угол наклона поверхности, рад.,

t — время с момента начала разлива, с.,

R — коэффициент, учитывающий свойства жидкости и поверхности.

Для точечного источника при наклонной поверхности используется это выражение (8):

Где:

x_N​(t) — протяжённость разлива в момент времени t, м.,

ξ_N ​ — безразмерная константа, зависящая от типа разлива и источника,

V — объём разлитой жидкости, м³.,

θ_s — угол наклона поверхности, рад.,

t — время с момента начала разлива, с.,

R — коэффициент, учитывающий свойства жидкости и поверхности.

Модуль инфильтрации в Oil Surface Flow Screening Model основана на модели Грина–Ампта которая является приближением процесса избыточного впитывания, представленном на рисунке 1. [2]

Рис.1. Образование избыточного инфильтрационного стока в природе.

На рисунке 1 последовательные профили влажности почвы показаны в виде кривых, где (а) — содержание влаги в зависимости от профилей глубины, (б) — временной ряд образования поверхностного стока, а (в) — фронт смачивания в песчаной почве, обнаженной после сильного дождя причём содержание влаги постепенно уменьшается до исходного уровня ниже фронта увлажнения. Модель Грина–Ампта упрощает эти кривые профили влажности до резкого интерфейса с условиями насыщения, θ = n, выше фронта увлажнения и начальным содержанием влаги, θ = θ₀, ниже фронта увлажнения (рисунок 2). Предполагается, что начальное содержание влаги по глубине однородно. Обозначим глубину фронта увлажнения через L. Разность между насыщенным и начальным содержанием влаги обозначим Δθ = n – θ₀. Тогда глубина инфильтрации воды после начала процесса впитывания равна:

Где:

F — общая глубина инфильтрированной жидкости, см.,

L ​ — глубина фронта смачивания, см.,

θ — содержание влаги.

За основу определения гидравлической силы принимается поверхность, также предполагается неограниченный приток воды на поверхность при малой глубине затопления, поэтому вклад этой глубины в гидравлический градиент не учитывается. Сразу под фронтом увлажнения, на глубине чуть большей, чем L, почва находится в исходном ненасыщенном состоянии с соответствующей силой всасывания |ψ_f|. Разность гидравлических сил, создающая движение воды от поверхности до точки сразу под фронтом, равна:

Где:

h — Разность гидравлических сил,

ψ_f — капиллярное давление на фронте, см.,

L ​ — глубина фронта смачивания, см.

Гидравлический градиент получается делением этой разности сил на расстояние L от поверхности до фронта увлажнения:

Где:

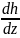— Гидравлический градиент,

ψ_f — капиллярное давление на фронте, см.,

L ​ — глубина фронта смачивания, см.

Рис.2. Идеализация модели Грин–Эмпта: фронт увлажнения проникает в профиль почвы.

Подставляя это (11) в уравнение Дарси, получаем выражение для пропускной способности инфильтрации:

Где:

f_с — пропускная способность инфильтрации

Kₛₐₜ — Коэффициент фильтрации, см/ч.,

P — капиллярный потенциал, см.,

F — общая глубина инфильтрированной жидкости, см.,

ψ_f — влажность почвы, см.,

θ — содержание влаги.

L ​ — глубина фронта смачивания, см.

Здесь во втором равенстве использовано соотношение (9), 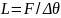. Получается функция убывания пропускной способности инфильтрации . Параметры этой модели — и . Используя характеристику влажности почвы ψ_f можно оценить как:

Где: — модуль капиллярного давления на фронте смачивания, см.,

θ₀ — начальное содержание влаги.

Начальное содержание влаги θ₀ может быть принято равным полевой (θ_fc) или предельно увядающей (θ_pwp) точке в зависимости от предшествующих условий. Оценку |ψ_f| можно взять через давление начала воздушного проникновения:

Где:

— модуль капиллярного давления на фронте смачивания, см.,

|ψ_a| и b — табличные параметры.

Такое упрощение обычно достаточно для гидрологических расчётов. В таблице 1 приведены параметры инфильтрации по Грин–Ампту для различных классов текстур почвы.

Таблица 1. Параметры инфильтрации по модели Грин–Ампта для различных классов текстур почв. Числа в скобках — ±1 стандартное отклонение.

Состав почвы [3]	Пористость, n	Эффективная пористость, θₑ	Напор на фронте смачивания, |ψf| (см)	Коэффициент фильтрации, Kₛₐₜ (см/ч)
Песок: 85–100 % Ил: 0–15 % Глина: 0–10 %	0.437 (0.374–0.500)	0.417 (0.354–0.480)	4.95 (0.97–25.36)	11.78
Песок: 70–85 % Ил: 0–30 % Глина: 0–15 %	0.437 (0.363–0.506)	0.401 (0.329–0.473)	6.13 (1.35–27.94)	2.99
Песок: 43–85 % Ил: 0–50 % Глина: 0–20 %	0.453 (0.351–0.555)	0.412 (0.283–0.541)	11.01 (2.67–45.47)	1.09
Песок: 23–52 % Ил: 28–50 % Глина: 7–27 %	0.463 (0.375–0.551)	0.434 (0.334–0.534)	8.89 (1.33–59.38)	0.34
Песок: 0–50 % Ил: 50–88 % Глина: 0–27 %	0.501 (0.420–0.582)	0.486 (0.394–0.578)	16.68 (2.92–95.39)	0.65
Песок: 45–80 % Ил: 0–28 % Глина: 20–35 %	0.398 (0.332–0.464)	0.330 (0.235–0.425)	21.85 (4.42–108.0)	0.15
Песок: 20–45 % Ил: 15–53 % Глина: 27–40 %	0.464 (0.409–0.519)	0.309 (0.279–0.501)	20.88 (4.79–91.10)	0.1
Песок: 0–20 % Ил: 40–73 % Глина: 27–40 %	0.471 (0.418–0.524)	0.432 (0.347–0.517)	27.30 (5.67–131.50)	0.1
Песок: 45–80 % Ил: 0–20 % Глина: 35–55 %	0.430 (0.370–0.490)	0.321 (0.207–0.435)	25.12 (4.08–140.2)	0.06
Песок: 0–20 % Ил: 40–60 % Глина: 40–60 %	0.479 (0.425–0.533)	0.423 (0.354–0.516)	29.22 (6.13–149.4)	0.05
Песок: 0–45 % Ил: 0–40 % Глина: 40–100 %	0.475 (0.427–0.523)	0.385 (0.269–0.501)	31.63 (6.39–156.5)	0.03

При заданной скорости подачи поверхностной воды w, накопленная инфильтрация до затопления равна F = w t. Затопление наступает, когда пропускная способность инфильтрации падает до уровня подачи, . Подставляя в (12) и решая относительно F, получаем накопленную инфильтрацию к моменту затопления:

Где: F_p — совокупная инфильтрация до начала поверхностного стока, см.,

K_sat — насыщенная гидравлическая проводимость почвы, см/ч.,

|ψ_f| — модуль капиллярного давления на фронте смачивания, см.,

Δθ — разность между насыщенной и начальной влажностью почвы, безразмерная величина,

w — интенсивность осадков, см/ч.

Соответственно, время до затопления рассчитывается следующим образом (16):

Где: t_p — время до начала поверхностного стока, ч.,

F_p — совокупная инфильтрация до начала поверхностного стока, см.,

w — интенсивность осадков, см/ч.,

K_sat — насыщенная гидравлическая проводимость почвы, см/ч.,

|ψ_f| — модуль капиллярного давления на фронте смачивания, см.,

Δθ — разность между насыщенной и начальной влажностью почвы, безразмерная величина

Для решения задачи инфильтрации после установления режима затопления в модели Грина–Ампта следует учесть, что скорость инфильтрации равна производной от накопленной инфильтрации и ограничена инфильтрационной способностью:

Где:

f(t) — скорость инфильтрации в момент времени t, см/ч.,

— производная совокупной инфильтрации по времени, см/ч.,

K_sat — насыщенная гидравлическая проводимость почвы, см/ч.,

|ψ_f| — модуль капиллярного давления на фронте смачивания, см.,

Δθ — разность между насыщенной и начальной влажностью почвы, безразмерная величина,

F — совокупная инфильтрация, см.

Здесь явно показана зависимость от времени. Подставляя в это выражение уравнение (12), получаем следующее дифференциальное уравнение:

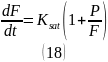
Где:

— скорость изменения совокупной инфильтрации по времени, см/ч.,

K_sat — насыщенная гидравлическая проводимость почвы, см/ч.,

P — параметр, равный произведению |ψ_f| и Δθ, см.,

F — совокупная инфильтрация, см.

С помощью метода разделения переменных это уравнение интегрируется от начальной накопленной инфильтрации F_s​ в момент времени t_s​ до некоторого значения F в момент t. В результате получается выражение для накопленной инфильтрации при затопленном режиме:

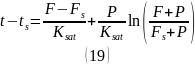
Где:

t — текущее время, ч.,

t_s — время начала насыщения почвы, ч.,

F — совокупная инфильтрация в момент времени t, см.,

F_s — совокупная инфильтрация в момент времени t_s, см.,

K_sat — насыщенная гидравлическая проводимость почвы, см/ч.,

P — параметр, равный произведению |ψ_f| и Δθ, см.

Прямого аналитического решения для F из этого уравнения не существует, однако при подстановке t_s = t_p и F_s = F_p его можно численно решить для любого t > t_p ​, что даёт зависимость накопленной инфильтрации от времени.

Ключевая идея модели Грина–Ампта заключается в том, что инфильтрационная способность во время осадков уменьшается с ростом накопленной глубины инфильтрации. Это приводит к снижению скорости инфильтрации и, соответственно, к увеличению доли стока по поверхности с течением времени, что хорошо согласуется с эмпирическими наблюдениями. Поскольку скорость инфильтрации зависит от накопленной глубины, последняя может рассматриваться как состояние системы, и модель естественным образом учитывает переменную интенсивность осадков и изменяющуюся скорость потери способности к инфильтрации. Этот подход называют «приближением инфильтрабельности-глубины»

В Oil Surface Flow Screening Model инфильтрация жидкости в грунт определяется взаимодействием воздуха, масла и воды. Уравнения для инфильтрации нефти в зонe аэрации нелинейны и связаны с уравнениями течения воды и воздуха. Глубина фронта инфильтрации 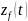при времени определяется из модели Грина–Ампта (19):

Где:

n — пористость,

K₁ — проводимость почвы для нефти,

S₁ — насыщение позади фронта,

h — толщина плёнки,

H_f — высота фронта.

Затем объемный поток на единицу площади разлива, q_i, можно оценить из выражения (21)

Где:

K₁ — проводимость почвы для нефти,

z_f — глубина фронта инфильтрации

S₁ — насыщение позади фронта,

h — толщина плёнки,

H_f— высота фронта.

Испарение жидкости зависит от условий разлива и состава. Модель Oil Surface Flow Screening Model применима как к чистым жидкостям, так и к смесям летучих компонентов.

Для чистой жидкости:

Где:

k_g — коэффициент массообмена в газовой фазе,

v — мольный объём жидкости,

P — давление насыщенных паров,

R — универсальная газовая постоянная,

T — температура.

Для смеси компонентов:

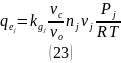
Где:

v_c — средний эффективный мольный объём нефти,

v_o — объём нефти,

k_gi — коэффициент массообмена для компонента ,

n_j — число молей,

v_j — мольный объём,

P_j — давление насыщенных паров компонента .

Заключение

В итоге можно выделить преимущества и недостатки модели:

Преимущества:

Учитывает и точечные, и линейные источники разлива.

Предоставляет пространственное распределение глубины инфильтрации.

Недостатки:

Не описывает фазу перераспределения жидкости в процессе инфильтрации.

Список литературы

1. S. M. Tauseef, R. Ramyapriya, Tasneem Abbasi, S. A. Abbasi Models for assessing the spread of flammable liquid spills and their burning // International Journal of Engineering, Science and Mathematics (UGC Approved). - 2017. - Том 6 Выпуск 8. - С. 154-184.

2. David G Tarboton At a Point Infiltration Models for Calculating Runoff. - 5-е изд. - Utah: Utah State University, 2003. - 52 с.

3. Sand? Clay? Loam? What Type of Soil Do You Have? // Gardeners URL:https://www.gardeners.com/how-to/what-type-of-soil-do-you have/9120.html?srsltid=AfmBOorpGD2ze4Xmizdhj46h0KNK 6ZSbeSLl9osOe4jZ1rMBiRx8VW1 (дата обращения: 23.05.2025).