
курсовая / TVIMC
.docx
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ
Ордена трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теория вероятности и прикладной математики»
Индивидуальное задание
по дисциплине «Теория вероятностей и математическая статистика»
Модуль №1
Выполнил:
Проверила:
Синева И.С.
Москва, 2024
Содержание
1.Постановка задачи 2
2. Описательная статистика 3
2.1 Построим гистограммы для выборок: 4
2.2 Проведём анализ асимметрии, разброса и выбросов по гистограммам: 5
2.3 Найдём основные выборочные числовые характеристики в excel: 6
3. Оценивание параметров 8
3.1 Опираясь на результаты п.1, выпишем несмещенные точечные оценки: 8
3.2 Найдём доверительные оценки параметров нормальных распределений и распределения Пуассона. 9
4. Проверка статистических гипотез 10
5.Вывод 13
1.Постановка задачи
Описательная статистика
Случайные
величины
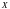 и
и
 распределены по нормальному закону
распределены по нормальному закону
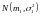 и
и
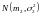 соответственно. Случайная величина
соответственно. Случайная величина
 имеет равномерное распределение
имеет равномерное распределение
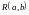 .
Случайная величина
.
Случайная величина
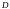 – дискретна и имеет распределение
Пуассона.
– дискретна и имеет распределение
Пуассона.
Требуется:
Просмотрев выборки
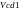 –
–
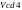 (
(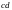 - номер варианта, соответствующий
номеру студента в журнале группы)
сформулировать и обосновать предположения
о том, какому из указанных распределений
соответствуют эти выборки.
- номер варианта, соответствующий
номеру студента в журнале группы)
сформулировать и обосновать предположения
о том, какому из указанных распределений
соответствуют эти выборки.Анализируя гистограммы частот, установить, какие данные более асимметричны, какие данные имеют наибольший разброс, какие данные содержат выбросы, сформулировать и обосновать предположения о том, какому из указанных распределений соответствуют эти выборки.
Найти основные выборочные числовые характеристики для массивов , , и :
объем выборки,
дисперсию,
среднее,
медиану,
нижнюю и верхнюю квартили,
моду,
коэффициенты асимметрии и эксцесса,
минимальное и максимальное значение,
размах выборки
По результатам пп. 1-2 определить, какие массивы соответствуют величинам с нормальным, равномерным и пуассоновским распределением. Ответ обосновать.
Оценивание параметров
Опираясь на результаты п.1, выписать несмещенные точечные оценки соответствующего предположительного распределения в каждом конкретном случае.
Найти доверительные оценки параметров нормальных распределений и распределения Пуассона.
Проверка статистических гипотез
Используя
критерий согласия
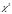 ,
проверить выдвинутые ранее предположения
о виде распределения каждой выборки.
,
проверить выдвинутые ранее предположения
о виде распределения каждой выборки.
Сделать обоснованные выводы из проведенного анализа.
2. Описательная статистика
Номер варианта – 25
Выбираем выборки v251,v252,v253,v254.

2.1 Построим гистограммы для выборок:


Предположим, что v252 это равномерное распределение, так как:
Все значения имеют примерно одинаковую вероятность появления.
На графике отсутствует выраженный пик.
v253 и v254 это нормальное распределение, так как:
Гистограмма имеет форму колокола
Большинство значений сосредоточено в центре, и чем дальше от центра, тем меньше значений.
v251 это Пуассоновское распределение, так как:
Гистограмма имеет форму, схожую с формой купола.
По диаграмме с точками видно что распределение дискретное.

2.2 Проведём анализ асимметрии, разброса и выбросов по гистограммам:

По графикам наибольшую асимметрию имеет выборка v251, затем идут v253, v254 и v252.
Проверим наблюдения с помощью формулы =СКОС(A:A) в excel:
v252 |
v253 |
v254 |
v251 |
0,048875 |
-0,00241 |
0,222265 |
0,222265 |
Распределения v252 и v253 почти симметричны
Распределения v254 и v251 имеют умеренную асимметрию, указывая на правостороннее смещение.
Наименьший разброс имеет выборка v252, остальные имеют больше разброс.
Проверим с помощью =СТАНДОТКЛОН(A:A) в excel:
v252 |
v253 |
v254 |
v251 |
0,592756 |
2,848975 |
1,086985 |
3,029686 |
Меньший разброс (v252) указывает на более однородную выборку данных
Больший разброс (v253, v254, и v251) говорит о том, что данные этих переменных более разнообразны, и в них присутствуют значения, сильно отличающиеся от среднего.
Выбросы есть на графике v253,v254,v251

Для выборки v253, точка 0 со значением 13,832
Для выборки v254, точка 0 со значениями 7,08; 7,547; 7,805
Для выборки v251, точка 0 со значением 19
Найдём основные выборочные числовые характеристики в excel:

v251 - Пуассоновское распределение
Дисперсия и среднее приблизительно равны (9,18 и 10,13), что характерно для Пуассоновского распределения.
Асимметрия положительная, что указывает на правостороннюю асимметрию распределения, что является признаком Пуассоновского распределения.
Эксцесс отрицательный, указывает на более плоский пик распределения по сравнению с нормальным распределением.
v252 - Равномерное распределение
Дисперсия относительно низкая (0,35), что может быть характерно для равномерного распределения, где значения распределены более равномерно, чем в других распределениях.
Коэффициент асимметрии близок к нулю, что указывает на симметричность распределения, а эксцесс отрицательный, что может указывать на равномерность.
v253 и v254 - Нормальное распределение
Среднее и медиана близки друг к другу, что является характерным признаком нормального распределения.
Асимметрия близка к нулю для обоих распределений, что указывает на симметрию распределений относительно среднего значения.
Эксцесс для v253 близок к нулю, что указывает на нормальность распределения. Для v254 эксцесс немного отрицательный, что может указывать на более плоский пик распределения, но всё ещё в пределах нормальности.
2.4 По полученным результатам делаем вывод, что v252 – равномерное распределение, v253 и v254 – нормальное распределение и v251 – Пуассоновское распределение.
3. Оценивание параметров
3.1 Опираясь на результаты п.1, выпишем несмещенные точечные оценки:
Рассчитаем с помощью excel:

Получаем:
Для v251:
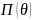
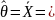 10,13
10,13
Для v252:
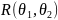
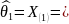 0,000119
0,000119
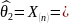 1,998422
1,998422
Для v253:
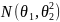
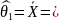 4,042855
4,042855
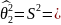 8,116658
8,116658
Для v254:
4,112403
1,181537
3.2 Найдём доверительные оценки параметров нормальных распределений и распределения Пуассона.
Для v251:
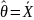
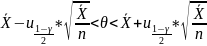
9,7075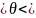 10,5525
10,5525
Для v253:
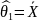
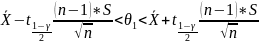
3,6456 4,4401
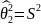
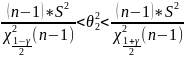
13,29039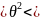 19,71459
19,71459
Для v254:
3,9608 4,2640
15,68821 18,18144
4. Проверка статистических гипотез
Используя критерий согласия , проверим выдвинутые ранее предположения о виде распределения каждой выборки в excel.
Проверка равномерности для v252:

Несмотря на то, что статистика превышает критическое значение при α = 0.05, ключевым фактором является p-value, который значительно превышает уровень значимости, что указывает на то, что нет достаточных оснований для отклонения нулевой гипотезы. v252 – равномерное распределение.
Проверка нормальности для v253:

P-value превышает установленный уровень значимости и значение статистики меньше критического значения, значит принимаем предположение о том, что v253 – нормальное распределение.
Проверка нормальности для v254:

P-value превышает установленный уровень значимости и значение статистики меньше критического значения, значит принимаем предположение о том, что v254 – нормальное распределение.
Проверка гипотезы о распределении Пуассона для v251:

P-value превышает установленный уровень значимости и значение статистики меньше критического значения, значит принимаем предположение о том, что v251 – Пуассоновское распределение.
5.Вывод
Проведён тщательный анализ четырёх выборок данных: v251, v252, v253 и v254, используя описательную статистику, гистограммы частот, а также расчёты основных выборочных числовых характеристик.
Выборка v252 была определена как равномерное распределение, что подтверждается отсутствием выраженного пика на гистограмме и приблизительно одинаковой вероятностью появления всех значений. Этот вывод подкреплён анализом асимметрии и дисперсии, указывая на наименьший разброс среди всех выборок и почти симметричное распределение. Проверка гипотезы с использованием критерия согласия не дала оснований для опровержения гипотезы, что выборка следует равномерному распределению.
Выборки v253 и v254 были определены как нормальное распределение. Это вывод основывается на форме гистограмм, которые напоминают колокол, с большинством значений, сосредоточенных в центре. Проверка гипотез с использованием критерия согласия не дала оснований для опровержения гипотезы, что обе выборки следуют нормальному распределению.
Выборка v251 была определена как распределение Пуассона на основании формы гистограммы и дискретного характера данных. Подтверждение этого предположения происходит через анализ асимметрии, который показал умеренную асимметрию, характерную для распределения Пуассона, а также наличие выбросов, что также может быть характерно для такого типа распределения. Проверка гипотез с использованием согласия не дала оснований для опровержения гипотезы, что выборка следуют Пуассоновскому распределению.
