
вопросы к экзамену / Zadachi_dlya_podgotovki
.docxВычислить определители


Найти произведение матриц
 ,
,

Вычислить ранг матриц

Построить матрицы, обратные данной
 .
.Решить систему методом Крамера

Решить систему методом Гаусса

Решить систему методом Гаусса.

Найти скалярное произведение векторов, если
 а
угол между векторами равен
а
угол между векторами равен
 .
.Найти модуль векторного произведения векторов, если их скалярное произведение равно 10,

Найти длины векторов и угол между векторами
 =(1,-3,-1)
=(1,-3,-1)
 =(2,1,-1).
=(2,1,-1).При каком α векторы =α
 2
2 +4
+4 ,
b ̅= (α, α, -2) будут перпендикулярны?
,
b ̅= (α, α, -2) будут перпендикулярны?При каких
 векторы
векторы
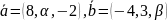 будут
коллинеарны?
будут
коллинеарны?Даны координаты точек А(1,2,2), В(0,-2, -3), С(2,-1, 0).Найти площадь треугольника АВС. Найти длину высоты, опущенной из вершины С.
Найти объем параллелепипеда, построенного на векторах = (1,2,-1), =2
 +
-3
,
+
-3
,
 ,
,
где А (-5, 2, -2), В (0, -2, 3).
Определить, при каком α, векторы
 будут
компланарны.
будут
компланарны.
Дана прямая x+6y-5=0. Определить какие из точек A(1,2), B(5, 0), C(6, -1), D(-7, 2),
E(-1,1), F(1, 1), G(0,4) принадлежат прямой, а какие не принадлежат. Найти расстояние от точек, не лежащих на данной прямой до этой прямой.
Даны уравнения прямых 5x-4y-3=0, 12x+5y-9=0. Найти угол между ними и координаты точки пересечения.
Даны координаты вершин треугольника A(2,-3), B(1, 4), C(0,1). Составить уравнение стороны AC, медианы AM и высоты, опущенной из вершины C.
Точка А (3, -4) – вершина квадрата. Сторона квадрата лежит на прямой
 Найти остальные вершины и составить
уравнения остальных сторон квадрата.
Найти площадь этого квадрата.
Найти остальные вершины и составить
уравнения остальных сторон квадрата.
Найти площадь этого квадрата.Найти площадь координатного угла, который прямая x+5y-7=0 отсекает от координатных осей.
При каких значениях параметра α и
 прямые αx-y-8=0, 25x-5y+
=0
прямые αx-y-8=0, 25x-5y+
=0
а) перпендикулярны, б) параллельны, в) совпадают.
Составить каноническое уравнение эллипса с
а) фокусным расстоянием 16 и малой полуосью 6;
б) фокусным расстоянием 48 и эксцентриситетом 12/13;
в) большая полуось равна16, а эксцентриситетом 2/3
г)
малая полуось равна 3 и точка М принадлежит эллипсу.
принадлежит эллипсу.
Определить, при каких значениях параметра прямая

а)
пересекает эллипс
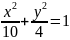
б) касается его;
в) проходит вне этого эллипса.
Составить каноническое уравнение гиперболы с
а) фокусным расстоянием 50 и мнимой полуосью 9
б) фокусным расстоянием 40 и эксцентриситетом 5/3;
в) действительная полуось равна16, а эксцентриситетом 4/3
г)
уравнения асимптот
 и точка М
и точка М принадлежит гиперболе.
принадлежит гиперболе.
Определить вид кривой второго порядка.




Найти нормальный вектор плоскости, проходящей через 3 точки A(1,3,2),B(8,0,4),С(1,5,3).
Дана плоскость x-2y+2z-6=0. Определить какие из точек A(7,1,2), B(0,5, 0), C(6, 0,0), D(2, -1, 1), E(-1,1,0), F(1, 1,1), G(0,4,7) принадлежат данной плоскости, а какие не принадлежат. Найти расстояние от точек, не лежащих на данной плоскости до этой плоскости.
Доказать, что плоскости параллельны и найти расстояние между плоскостями

Найти угол между плоскостями

Найти направляющие косинусы плоскости

Найти расстояние между плоскостями
При каких значениях параметра
 и
плоскости
и
плоскости

а) перпендикулярны, б) параллельны, в) совпадают.
Даны вершины треугольника A(1,3-,2),B(2,0,4),С(1,-1,3). Составить
а) каноническое уравнение стороны АС
б) параметрическое уравнение медианы АМ
в) уравнение высоты BH.
Найти угол между прямыми

При каких значениях параметра α прямые
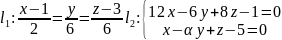
а) перпендикулярны, б) параллельны, в) совпадают.
При каких значениях параметра α прямая
 а) параллельна, б) пересекает в) лежит
в плоскости
а) параллельна, б) пересекает в) лежит
в плоскости

Найти расстояние от точки М (3, 2, -1) до прямой

Перечислить основные свойства и нарисовать схематически график
функции

Вычислить пределы функций.
а) b)
b)
 c)
c)

d)

e) g)
g)
 h)
h)

а)
 б)
б)

в)
 г)
г)
 д)
д)

40. Вычислить производные функций.
a)
 ,
b)
,
b)

c)
 d)
d)
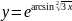
a)
 ,
b)
,
b)

c)
 d)
d)

41. Вычислить производные n-го порядка.
a)
 b)
b)

42. Вычислить пределы по правилу Лопиталя.
a)
 ,
b)
,
b)
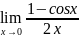
43.
Найти экстремумы функции:
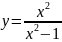
44.
Найти точки перегиба и направление
выпуклости функции

45.
Найти асимптоты функции:

46. Исследовать функцию на непрерывность

47. Исследовать функцию на непрерывность

48. Исследовать функцию и построить ее график

