18. В колебательной системе кроме консервативных сил Имеется активное сопротивление поэтому энергия колебательного контура будет расходоваться на преодоление этого сопротивления вследствие чего в колебательном контуре будут свободными и затух. U_R+U_L+U_C=0;

U_R=RI=Rq’; U_L=LdI/dt=Lq’’; U_C=q/c;

Lq’’+Rq’+q/c=0; q’’+Rq’/L+q/LC=0; [β=R/L, ω₀²=1/LC]; q’’+2βq’+ω₀²q=0-диф уравнение электромагнитных свободных затух колебаний. Решение: q=q₀e^-βtcos(ω₀+φ).

Любая колебательная система характеризуется добротностью. Добротность колебательной системы равна:

Q=2πW/∆W где W-энергия запасенная колебательной системы в момент времени t. ∆W-потеря энергии за 1 период.

 Дифференциальное уравнение свободных затухающих электромагнитных колебаний

 

В реальном контуре имеют место следующие потери энергии:

1) тепловые потери, так как ;

2) потери в диэлектрике конденсатора;

3) гистерезисные потери в сердечнике катушки;

4) потери на излучение и др.

Уравнение колебаний можно получить, исходя из того, что сумма падений напряжения на ёмкости, индуктивности и активном сопротивлении должна быть равна нулю:

 .                                                                                                      (8.7)

Разделив это выражение на L и заменив I через , а  через , получим

 .                                                                                                 (8.8)

Беря во внимание, что  равно квадрату собственной частоты контура ₀, вводим обозначение: , после этого уравнение принимает вид

 .                                                                                                 (8.9)

При условии, что , т. е. , уравнения имеет вид

 ,                                                                                             (8.10)

где . Подставив значение для ₀ и для , находим :

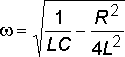 .                                                                                                         (8.11)

Таким образом, частота затухающих колебаний меньше собственной частоты ₀. Разделив выражение (8.10) на емкость С, получим напряжение на конденсаторе:

 .                                                                            (8.11)

 Амплитуда затухающих колебаний изменяется по закону , где А₀ – начальная амплитуда

Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна:

 .        

19. Вынужденные механические колебания:

Для того чтобы колебания были не затух необходимо либо периодично сообщать колебательной системе энергию равную потери энергии за один период, либо на колебательную систему действовать внешней силой изменяющейся по гармоническому закону. Такая сила называется возбужденной или вынужденной.

Пусть на пружинный маятник кроме сил: f_упр=-kx и f_сопр=-rx’ действует сила изменяющаяся по гармоническому закону F=F₀cosωt и эти силы направлены вдоль оси Х, тогда под действ равнодействующей этих трех сил, тело массой m приобретает ускорение a

mx’’=-kx-rx’+F₀cosωt;x’’+2βx+ω₀²x=F₀cosωt/m

-это ур-ие имеет решение x=A₀cos(ωt-φ)

Из формул видно что вынужденные колебания совершаются с частотой равной частоте вынужденной силы и с отставанием по фазе на угол φ. A₀=f(m,r,k,ω).

Резонансная частота.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к ча­стоте, равной или близкой собственной частоте колебательной системы, называется резонансом

20. Электромагнитные вынужденные колебания:

Для того чтобы колебания в контуре были не затух – подключим к нему последовательно источник синусоидального напряжения.

U_R+U_L+U_C=U₀cosωt; F=qE; T>>t=l/c

q’’+2βq’+ω²q=U₀cosωt/L-дифференциальное уравнение ие вынужденных электромагнитных колебаний Решение: q=q₀cos(ωt+φ)

q₀=f(ω). 1.ω=0 q₀=U₀/Lω₀² 2. β=0

q₀=U₀/L(ω₀²-ω²). 3. β≠0

Чтобы в Чтобы в реальной колебательной системе осуществлять незатухающие колебания, надо компенсировать каким-либо потери энергии. Такая компенсация возможна, если использовать какой-либо периодически действующего фактора X(t), который изменяется по гармоническому закону:

При рассмотрении электрического колебательный контура роль X(t) играет подводимая к контуру внешняя соответсвующим образом периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение   (3)  Тогда дифференциальное уравнение колебаний заряда Q в простейшем контуре, используя (3), можно записать как    Зная формулу циклической частоты свободных колебаний колебательного контура и формулу предыдущего раздела (11), придем к дифференциальному уравнению   (4)  Колебания, которые возникают под действием внешней периодически изменяющейся э.д.с., называютсявынужденными электромагнитными колебаниями. 

 (5) 

причем далее мы будем применять его решение для вынужденных колебаний в зависимости от конкретного случая (x₀ если механические колебания равно F₀/m, в случае электромагнитных колебаний - U_m/L).  Решение уравнения (5) будет равно (как известно из курса дифференциальных уравнений) сумме общего решения (5) однородного уравнения (1) и частного решения неоднородного уравнения. Частное решение ищем в комплексной форме. Заменим правую часть уравнения (5) на комплексную переменную х₀e^iωt :   (6)  Частное решение данного уравнения будем искать в виде    Подставляя выражение для s и его производных (  и  ) в выражение (6), найдем   (7)  Поскольку это равенство должно быть верным для всех моментов времени, то время t из него должно исключаться. Значит η=ω. Учитывая это, из формулы (7) найдем величину s₀ и умножим ее числитель и знаменатель на (ω₀² - ω² - 2iδω)    Это комплексное число представим в экспоненциальной форме:    где   (8)   (9)  Значит, решение уравнения (6) в комплексной форме будет иметь вид    Его вещественная часть, которая является решением уравнения (5), равна   (10)  где А и φ определяются соответственно формулами (8) и (9).  Следовательно, частное решение неоднородного уравнения (5) равно   (11)  Решение уравнения (5) есть сумма общего решения однородного уравнения   (12) 

Запишем выражения (10), (8) и (9) для электромагнитных колебаний, учитывая, что ω₀² = 1/(LC) и δ = R/(2L) :   (13)    Продифференцировав Q=Q_mcos(ωt–α) по t, получим силу тока в контуре при установившихся колебаниях:   (14)  где   (15)  Уравнение (14) может быть записано как    где φ = α – π/2 — сдвиг по фазе между током и приложенным напряжением (см. (3)). В соответствии с уравнением (13)   (16) 

21.Если колебательное тело находится в упругой среде то оно приводит в колебательное движение частицы среды соприкасающихся с этим телом, в результате упругого взаимодействиия частиц среды, в колебательном процесс вовлекаютя и более удаленные частицы среды. Процесс распределения колебательного движения в упругой среде называется волной В процессе распространения волны не происходит перенос частиц среды, они лишь колеблются возле положения своего равновесия, перенос вещества не происходит В зависимости от направления колебания частиц среды по отношению к направлению распространения волны, волны подразделяются на поперечные и продольные. В однородной среде волна распространяется с пост V, лямбда=Vt. Геометричекое место точек до которых дошла волна к мом врем t называется фронтом волны. Фронт волны разделяет ту часть пространства в которой частицы не совершают колебаний от той где совершают. Геометрическое место точек колебаний в одинаковой фазе называется фазовой поверхностью. Фазовая поверхность проходит ч/з положение равновесия частиц колеблющихся в одинаковой фазе, в отличие от фронта волны фазовые поверхности неподвижны и их множество. В зависимости от вида, формы волны фронты бываютплоскими и сферическими. Для описания волнового процесса в среде треб найти амплитуду и фазу колебаний различных точек среды и изменения их по времени. Ур-ем волны называется математическое выражениие которое задает смещения точек среды как функцию их координаты. ξ(x,y,z,t)=0 Рассмотрим одномерн синусоид плоскую волну распространяющуюся вдоль оси Х. х=0; ξ(0;t)=asin(ωt+φ); среда не погл a=const, за время τ→x=Vτ;

x→ξ(x,t)=asin[ω(t-τ)+φ]; ξ(x,t)=asin[ω(t-x/V)+φ]; с учетом ω=2π/T; VT=λ; 2π/λ=k;

ξ(x,t)=asin(ωt-kx+φ)-ур-е плоской одномерной волны. Где к-называется волновым числом, оно показывает сколько длин волн λ откладывается на отрезке 2π метров. Рассмотрим сферическую волну: в процессе распространения сфер волны за равные промежутки времени в колебательное движение вовлекаются частицы среды в возрастающи х объемах ω↓; a↓; ξ(r,t)=asin(ωt-kr+φ)/r – справедливо при усл r>>d (d-диам ист-а сфер волн). Уравнение плоской волны является решением дифференциального уравнения называемого го волновым уравнением: ξ(x,y,z,t)=asin(ωt-k_xx-k_yy-k_zz+φ); где k_x k_y k_z-проекции волнового вектора k на оси декартовые координат.

22.Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова

уравнение колебаний частиц, лежащих в плоскости х, имеет вид

                                                         (154.1)

откуда следует, что(х, t)  является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

                                     (154.2)

где А = const — амплитуда волны,  — циклическая частота, ₀ — начальная фаза вол­ны, определяемая в общем случае выбором начал отсчета х и t,[ (t—x/v)+ ₀] — фаза плоской волны.

Для характеристики волн используется волновое число

                                                         (154.3)

Учитывая (154.3), уравнению (154.2) можно придать вид

                                         (154.4)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx.

Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде

где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е.

                                                           (154.5)

Продифференцировав выражение (154.5) и сократив на , получим  откуда

                                                                     (154.6)

Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.

Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как

                                    (154.7)

где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r. Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Из выражения (154.3) вытекает, что фазовая скорость

                                                        (154.8)

Если фазовая скорость воли в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных

или

                                                

23. Если в пространстве имеется переменное электрическое поле то оно порождает переменное магнитное поле, в свою очередь переменное магнитное поле создает перемещение электрического поля. Силовые линии первичного поля концентрически охватываются силовыми линиями вторичного поля. В результате чего образуется система переплетенных м/у собой переменных вихревых электрических и магнитныхполей те электромагнитное поле. Вторичное поля первоначально связаны с движущимися зарядами и токами, в дальнейшем они могут оторваться от них и породить друг друга в виде волны, которая называются электромагнитной волной. Если преобразовать 1 и 2 ур-ие Максвелла для ρ=0,σ=0,ε=const, μ=const приводят к:

каждое из этих уравнений является волновым. Сравним ур-е (3) с ур-ми для волн в упругой среде, можно сделать следующие выводы:

Плоская электромагнитная волна: Вдали от источника совершает sin-ые колебания частотой ω, электромагнитную волну можно рассматривать как плоскую. Решение ур-я (3) при распространении электромагнитной волны вдоль оси Х имеет след вид:

Из (5)→что E и H колеблются во в заимно перпендикулярных плоскостях, перпендикулярно распространению волны. Эл магн волна является поперечной. Эл магн волна распространяясь в пространстве переносит энергию объемная плотность которой складывается W=W_э +W_м=εε₀E²/2+μμ₀H²/2. E и H связаны соотн εε₀E²=μμ₀H² –(7). С учетом (7) W= εε₀E²= =μμ₀H²=EH/V; WV=EH; WV=S-вектор Поинтинга. S=WV=E ^x H. →1.S↑↑ox 2. По модулю вектор Поинга равен энергии переносимой электро

магнитной волной за единицу врем через единицу поверхности распространения перпендикулярно к распространению волны