Лекция 8 Усилители с емкостной связью. Избирательные усилители

8.1 Усилители с емкостной связью

В некоторых случаях усиливаемый сигнал содержит переменную и постоянную составляющие, при чём информативной является только переменная составляющая на фоне значительной постоянной. Усилить переменную составляющую с помощью УПТ невозможно, т.к. усилитель окажется в насыщении под действием постоянной составляющей сигнала. Для устранения постоянной составляющей между источником сигнала и входом усилителя включают разделительный конденсатор. Возможны инвертирующая (рисунок 7.18) и неинвертирующая (рисунок 7.20) схемы включения ОУ.

8.1.1 Инвертирующая схема с ёмкостной обратной связью

Коэффициент усиления с обратной связью для схемы показанной на рисунке 8.1 носит комплексный характер, в области низких частот определяется выражением

(8.1)

Рисунок 8.1 - Инвертирующий усилитель с ёмкостной связью

Модуль зависит от частоты и постоянной времени входной цепи в области низких частот

(8.2)

где - модуль коэффициента усиления в области средних частот.

Эту зависимость называют амплитудно-частотной характеристикой, её строят в логарифмическом масштабе (рисунок 8.2) для области низких частот по уравнению

(8.3)

где - частота нижнего среза.

Рисунок 8.2- Логарифмическая амплитудно-частотная характеристика инвертирующего усилителя с ёмкостной связью

Для удобства построения амплитудно-частотной характеристики аппроксимируется тремя прямыми:

прямая 1 (рисунок 8.2) проводится параллельно оси частот на уровне , она соответствует диапазону средних частот

прямая 2 соответствует области низких частот при

, (8.4)

эти прямые будут пересекаться в точке при .

Прямая 3 соответствует области высоких частот, в которой зависит от частотных свойств операционного усилителя и определяется выражением

, (8.5)

где - частота верхнего среза,

- частота единичного усиления.

Точке пересечения прямых 1 и 3 будет соответствовать частота верхнего среза .

Прямые 2 и 3 имеют угол наклона на декаду.

К основным частотным параметрам для широкополосных усилителей относятся коэффициенты частотных искажений в области низких частот

(8.6)

коэффициенты частотных искажений в области высоких

(8.7)

Входное и выходное сопротивления усилителя с ёмкостной связью определяются в области средних частот по выражениям

, (8.8)

(8.9)

8.1.2. Неинвертирующий усилитель с ёмкостной связью

В схему неинвертирующего усилителя с ёмкостной связью (рисунок 8.3) входят: разделительный конденсатор , резистор, который создаёт путь для протекания входного тока смещения; резисторыи, которые задают коэффициент усиления, и конденсатор, который служит для уменьшения напряжения сдвига.

Рисунок 8.3 - Неинвертирующий усилитель с емкостной связью

Коэффициент усилия с обратной связью неинвертирующего усилителя находится как

(8.10)

где первый сомножитель определяет коэффициент деления делителя образованного конденсатором и резистором, а второй сомножитель определяет коэффициент усилия сигнала после делителя.

Модуль коэффициента усилия после преобразований получим в следующем виде

(8.11)

где

(8.12)

(8.13)

(8.14)

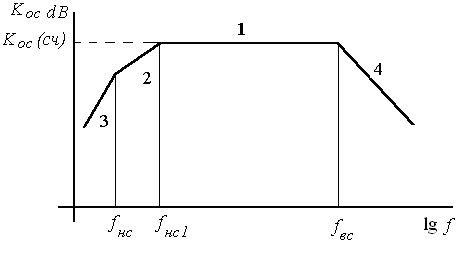
Рисунок 8.4 - Логарифмическая амплитудно-частотная характеристика неинвертирующего усилителя с ёмкостной связью

Логарифмическая амплитудно-частотная характеристика в области низких частот аппроксимируется тремя прямыми:

• прямая 1 (рисунок8.4)

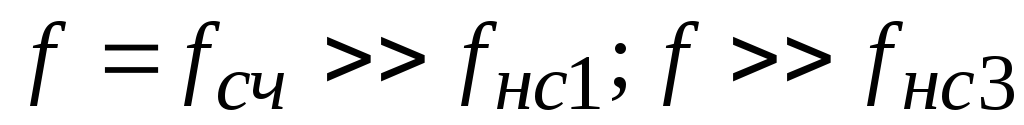
соответствует области средних частот;

• прямая 2

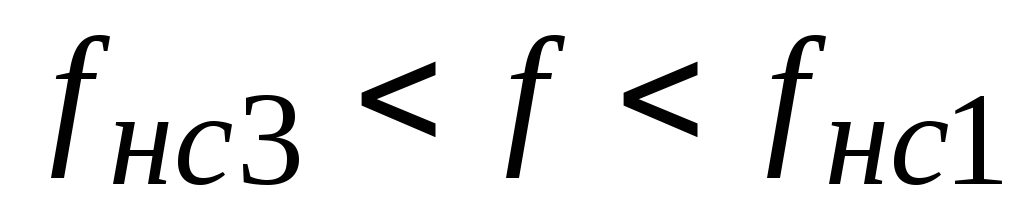
(8.15)

имеет угол наклона на декаду;

• прямая 3

(8.16)

имеет наклон на декаду.

В области высоких частот логарифмическая амплитудно-частотная характеристика строится также как для неинвертирующего усилителя ( прямая 4).

Выходное сопротивление неинвертирующего усилителя с ёмкостной связью в области средних частот определяется выражением (1.48).

Входное сопротивление равно параллельному соединению резистора и входного сопротивления неинвертирующего каскада (1.47), которое много больше. Следовательно.

Коэффициент частотных искажений в области низких частот

, (8.17)

как видно из (8.12) и (8.13) зависит от ёмкости конденсаторов и.