Единичная функция Хевисайда

Простейшей функцией-оригиналом является так называемая единичная функция Хевисайда, имеющая вид

Нетрудно видеть, что если умножить функцию на единичную, то результат умножения гасит функциюдляи оставляет ее без изменения для. Таким образом, если функцияудовлетворяет приведенным выше условиямI и III, но не удовлетворяет условию II, то произведение

уже будет удовлетворять и условию II, а функция будет оригиналом. Примерами могут служить функциии т.д. Для простоты записи обычно, как правило, опускают множитель, принимая во внимание, что все рассматриваемые нами функции-оригиналы равны нулю для. В связи с этим вместобудем писать единицу, вместобудем писать простои т.д.

График единичной функции приведен на рис.1. Ее изображение, очевидно, будет:

Более общая функция вида

где вещественное неотрицательное число, называется запаздывающей единичной функцией. Ее изображение будет:

График запаздывающей единичной функции приведен на рис. 2.

Некоторые основные свойства преобразования Лапласа

Рассмотрим некоторые основные свойства преобразования Лапласа:

1. Свойство линейности. Изображение суммы конечного числа оригиналов, умноженных на постоянные величины, равно сумме изображений этих оригиналов, умноженных на те же постоянные величины:

Доказательство. Это свойство линейности вытекает непосредственно из определения изображения, даваемого равенством (1). Пусть , где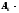постоянные. Положим, что. Тогда будем иметь:

Следовательно, .

2. Теорема подобия. Для всякой постоянной величины имеет место соотношение

Доказательство. Найдем изображение функции .

Отсюда следует, что .

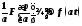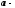3. Теорема смещения. Для всякой постоянной величины , гдевещественное или комплексное число имеет место соотношение

Доказательство. Найдем изображение функции .

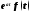, отсюда следует

Дифференцирование и интегрирование оригинала

Дифференцирование оригинала. Если является оригиналом, то справедливо соотношение

Доказательство. Найдем изображение

.

В частном случае, если 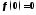, то будем иметь

Соотношения (9) и (10) легко обобщаются. В самом деле, интегрируя два раза по частям , получим:

.

Применяя то же свойство раз, найдем:

В частном случае, когда , то из (11) получим:

Интегрирование оригинала. Если , то справедливо соотношение

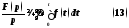
Доказательство. Обозначим и найдем изображение. Будем иметь

Зная, что , получим из равенства

, т.е. ., т.к.

. Следовательно, , т.е.

Дифференцирование и интегрирование изображений

Дифференцирование изображения. Дифференцирование изображения функции соответствует умножению оригинала на .

Доказательство.В самом деле, пусть или. Возьмем ряд производных отпо, тогда будем иметь:

,

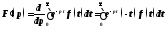откуда

.

Для второй производной имеем: , отсюда имеем

.

Продолжая так и далее, получим

Интегрирование изображения. Интегрирование изображения функции по параметру в пределах отдосоответствует делению наоригинала функции, т.е.

Доказательство.Проинтегрируем по в пределах отдообе части равенства. Будем иметь

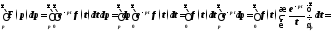
Следовательно, имеем ,

Теорема запаздывания

Теорема запаздывания. Для любого положительного τ имеет место соотношение

Доказательство. Пусть . Рассмотрим функциютакую, что

. Найдем изображение функции . Будем иметь

Следовательно, .

Теорема запаздывания показывает, что умножение изображения на сдвигает график оригинала вправо на(рис.3). Теорема запаздывания играет важную роль в операционном исчислении в связи с тем, что с ее помощью можно получать изображения функций, часто встречающихся в технических приложениях. К таким функциям относятся такие, которые имеют различные аналитические выражения в различных промежутках значений аргумента. Методы операционного исчисления позволяют производить действия с такими функциями особенно эффективно, что составляет его ценное преимущество. Теорема запаздывания успешно используется для получения изображений ступенчатых и периодических функций.

Теорема свертывания

Сверткой двух функций иназывается функция, для которой имеет место равенство

Операция получения свертки называется свертыванием функций. Свертку функций и обозначают символом.

Теорема свертывания. Если и, то

Доказательство. Найдем изображение свертки (16), для чего применим к ней преобразование Лапласа. Будем иметь

В правой части (18) переменим порядок интегрирования, для чего воспользуемся известной формулой Дирихле: , гдепроизвольная функция, непрерывная в треугольнике, ограниченном прямыми:. Тогда получим

. Следовательно,

.

Нетрудно видеть, что функции ив (19) можно поменять местами.

З а м е ч а н и е 1. Напомним формулу Дирихле. Она имеет вид :

где 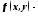произвольная функция, непрерывная в треугольнике, ограниченном прямыми:. Справедливость формулы Дирихле непосредственно следует из рис.4. Нетрудно видеть, что когда мы применили формулу Дирихле к выражению, то положили: