
- •Министерство образования и науки российской федерации
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами
- •Область в комплексной плоскости
- •Основы операционного исчисления Преобразование Лапласа и его основные свойства Понятие о преобразовании Лапласа. Прямое и обратное преобразования Лапласа
- •Единичная функция Хевисайда
- •Некоторые основные свойства преобразования Лапласа
- •Понятие о применении преобразования Лапласа к решению дифференциальных уравнений
- •Нахождение оригиналов функции по изображениям.
- •Применение операционных методов к решению дифференциальных
- •Уравнений
- •Вторая теорема разложения Хевисайда. Случай простых корней
- •Случай кратных корней
- •Решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами
- •Решение некоторых линейных дифференциальных уравнений с переменными коэффициентами
- •Интеграл Дюамеля
- •Исследование переходных процессов в электрических цепях методом операционного исчисления
Министерство образования и науки российской федерации
Филиал федерального государственного бюджетного образовательного учреждения
высшего профессионального образования «Уфимский государственный нефтяной
технический университет» в г. Салавате
КУРС ЛЕКЦИИ ПО РАЗДЕЛАМ МАТЕМАТИКИ
«Комплексные числа»
«Операционное исчисление»
Составитель: Хазиев Ф.М.
Салават 2012
КОМПЛЕКСНЫЕ ЧИСЛА
Комплексные числа и действия над ними
Комплексным
числом
 называется выражение вида
называется выражение вида (алгебраическая форма комплексного
числа), где
(алгебраическая форма комплексного
числа), где и
и - любые действительные числа,
- любые действительные числа, мнимая
единица, удовлетворяющая условию
мнимая
единица, удовлетворяющая условию .
Заметим, что
.
Заметим, что


Числа
 и
и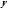 называются соответственно действительной
и мнимой частями комплексного числа
называются соответственно действительной
и мнимой частями комплексного числа и обозначаются
и обозначаются .
.
 Комплексное
число
Комплексное
число
 называетсясопряженным
комплексному числу
называетсясопряженным
комплексному числу
 .
Комплексные числа
.
Комплексные числа и
и считаются равными тогда и только тогда,
когда
считаются равными тогда и только тогда,
когда .
Комплексное число
.
Комплексное число изображается в плоскости
изображается в плоскости точкой
точкой ,
либо вектором
,
либо вектором ,
начало которого находится в начале
координат, а конец в очке
,
начало которого находится в начале
координат, а конец в очке (рис.1). Длина вектора
(рис.1). Длина вектора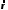 называется модулем комплексного числа
и обозначается
называется модулем комплексного числа
и обозначается ,
так что
,
так что .
Угол
.
Угол ,
образованный вектором
,
образованный вектором и осью
и осью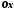 ,
называется аргументом комплексного
числа
,
называется аргументом комплексного
числа и обозначается
и обозначается ;
он определяется не однозначно, а с
точностью до слагаемого, кратного
;
он определяется не однозначно, а с
точностью до слагаемого, кратного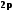 :
: ,
где
,
где есть главное значение
есть главное значение ,
определяемое условиями
,
определяемое условиями ,
причем
,
причем

Тригонометрическая форма комплексного числа
Из
рис.1 следует
 ,
следовательно
,
следовательно .
.
Тригонометрическая форма комплексного числа имеет вид

Действия над комплексными числами
Пусть
даны два комплексных числа: в алгебраической
форме
 и
и
 или в тригонометрической форме
или в тригонометрической форме и
и
1)
Сложение
(вычитание).
Суммой (разностью)
 двух
комплексных чисел называется комплексное
число
двух
комплексных чисел называется комплексное
число ,
определяемое равенством:
,
определяемое равенством:
 .
.
2)
Умножение.
Произведением
 двух комплексных чисел называется
комплексное число, определяемое
равенством:
двух комплексных чисел называется
комплексное число, определяемое
равенством:
 ,
,
т.е.
комплексные числа можно умножать по
правилу умножения многочленов, считая
при этом, что
 .
.
Если числа даны в тригонометрической форме, то



 ;
;
Следовательно, при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
3)
Деление.
Деление - действие, обратное умножению.
Разделить комплексное число
 на комплексное число
на комплексное число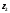 значит найти такое комплексное число
значит найти такое комплексное число ,
чтобы выполнялось равенство
,
чтобы выполнялось равенство или
или .
Перемножив левую часть получим:
.
Перемножив левую часть получим: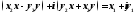 ,
откуда получаем систему уравнений
относительно
,
откуда получаем систему уравнений
относительно и
и :
:
 ,
,
которая
при
 всегда однозначно разрешима, т.к.
определитель
всегда однозначно разрешима, т.к.
определитель
 .
.
 ,
, .Тогда
по формулам Крамера имеем:
.Тогда
по формулам Крамера имеем:

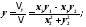 Тогда
Тогда
 называется
частным двух чисел
называется
частным двух чисел
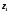 и
и и обозначается символом
и обозначается символом .
Заметим, что этот же результат можно
получить умножив числитель и знаменатель
на
.
Заметим, что этот же результат можно
получить умножив числитель и знаменатель
на .
.
Если эти числа заданы в тригонометрической форме, то
 ;
;
Таким образом, модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного равен разности аргументов делимого и делителя.
4)
Возведение
в степень.
Из правила умножения комплексных чисел,
заданных в тригонометрической форме,
следует правило возведения в целую
положительную степень
 комплексного числа
комплексного числа :
:

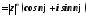 .Таким
образом
.Таким
образом

Эта формула называется формулой Муавра. Она показывает, что при возведении комплексного числа в целую положительную степень модуль возводится в эту степень, а аргумент умножается на показатель степени.
5)
Извлечение
корня.
Корнем
 ой
степени из комплексного числа
ой
степени из комплексного числа называется такое комплексное число
называется такое комплексное число ,
,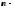 ая
степень которого равняется подкоренному
числу, т.е.
ая
степень которого равняется подкоренному
числу, т.е.
 ,
,
если
 ,
,
или
 .
.
Так
как у равных комплексных чисел модули
равны, а аргументы могут отличаться на
число, кратное
 ,
то
,
то .
Отсюда находим:
.
Отсюда находим:
 ,
,
где
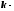 любое
целое число,
любое
целое число,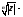 арифметическое
значение корня из положительного числа
арифметическое
значение корня из положительного числа .
Следовательно,
.
Следовательно,

Придавая
 значения
0, 1, 2, ... ,
значения
0, 1, 2, ... ,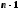 ,
получим
,
получим различных значений корня.
различных значений корня.
6)
Показательная
форма комплексного числа.
Из математического анализа известно
разложение функций
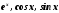 в степенной ряд:
в степенной ряд:

Условимся
считать, что формула (6) имеет место и
при
 ;
тогда получим
;
тогда получим
Учитывая (1) и отделяя действительные и мнимые члены, получим

На
основании формул (7) и (8) заключаем, что
сумма рядов, стоящих в скобках,
соответственно равна
 и
и ,
поэтому
,
поэтому

Формула (9) называется формулой Эйлера.

Решая
уравнения (9) и (10) относительно
 и
и ,
получим еще две формулы Эйлера
,
получим еще две формулы Эйлера

Формула (9) дает показательную форму комплексного числа:

