Министерство образования и науки Российской Федерации

Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Уфимский государственный нефтяной технический университет» в г. Салавате

(Филиал ФГБОУ ВПО УГНТУ в г. Салавате)

Кафедра «Общенаучные дисциплины»

СОГЛАСОВАНО УТВЕРЖДАЮ

Зав. кафедрой ОНД, доцент Зам. директора по учебной работе, доцент

_______________Т.М. Левина __________________Н.Н. Лунёва

_______________2014 __________________2014

Практикум по операционному исчислению

Дисциплина «Операционное исчисление»

СОГЛАСОВАНО Инженер по охране труда ___________ Г.В. Мангуткина ____________2014

РАЗРАБОТАЛ Профессор кафедры ОНД _____________Ф.М. Хазиев _____________2014

Салават 2013

В настоящем практикуме на многочисленных примерах подробно рассмотрены методы решения задач по операционному исчислению, включая операторный метод решения линейных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений. Даны образцы решения примеров и задач. Практикум предназначен для студентов направления подготовки 220700 «Автоматизация технологических процессов и производств».

Обсуждено на заседании кафедры ОНД

Протокол № ______ от ___________________2014

 Филиал ФГБОУ ВПО УГНТУ в г. Салавате, 2014

Содержание

1. Краткая теория работы 3

2. Методические указания и примеры выполнения заданий

по операционному исчислению 4

3. Варианты заданий 11

4. Список использованной литературы 20

Цель работы: приобретение навыков решения обыкновенных дифференциальных уравнений методами операционного исчисления.

Краткая теория работы

1.Основными понятиями операционного исчисления являются понятия оригинала и изображения.

ОПРЕДЕЛЕНИЕ. Функция , называется оригиналом, если она удовлетворяет трём условиям совместно:

а) при ;

б) постоянные и , для которых имеет место неравенство ;

в) на отрезке для , 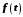может иметь не более, чем конечное число точек разрыва 1-го рода.

Преобразование Лапласа представляет собой линейное преобразование некоторой вещественной функции вещественного в другую функцию комплексного переменного и определяется по формуле

,

где оригинал, изображение.

Простейшим оригиналом является функция единичная функция Хевисайда

2.Основные свойства преобразования Лапласа. Если , то

2.1. Свойство линейности. ;

2.2. Теорема подобия. ;

2.3. Теорема смещения. ;

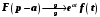2.4. Дифференцирование оригинала.

2.5. Дифференцирование изображения. ;

2.6. Интегрирование оригинала. ;

2.7. Интегрирование изображения. ;

2.8. Теорема запаздывания. ;

2.9. Теорема умножения (свёртывания) .

;

2.10. Формула Дюамеля .

Методические указания и примеры выполнения заданий по операционному исчислению

1. Найти изображение функции .

Сначала найдем изображение . Используя равенства и , имеем . Применяя теорему смещения , получим . Таким образом

.