
- •Практическая работа №2
- •Вариант №26
- •Построение модель вс в терминах иерархической сети Петри (сп)
- •Анализ сп модели через дерево достижимых разметок
- •Модифицируем модель сети петри
- •Устранение ошибок
- •Исследование сп-модели на основе матричных методов
- •Анализ сп-модели при помощи дерева достижимых разметок.
- •Демонстрация производительности модифицированной сп-модели
- •Заключение
Исследование сп-модели на основе матричных методов
С помощью матричных методов можно показать, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтверждается, то можно заключить, что описываемая система содержит некоторые недоработки.
Введем в рассмотрение матрицу С, которая поучается следующим образом:
C=HT-F, где HT - транспонированная матрица H.
Пусть размерность С равна n x m, где m и n - мощности множеств Р и Т.
C |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
t7 |
t8 |
t9 |
p1 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
p2 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
p3 |
-1 |
-1 |
1 |
1 |
0 |
0 |
-1 |
1 |
0 |
p4 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
p5 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
p6 |
0 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
p7 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
p8 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
p9 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
p10 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
p11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
p12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
p13 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
Далее
рассмотрим матричное уравнение:
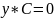 .
.
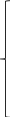 Согласно
этому уравнению, получаем:
Согласно
этому уравнению, получаем:
-y1-y3+y4 = 0
-y2-y3+y5 = 0
y3-y4+y6 = 0
y3-y5+y6 = 0
y1-y6+y7+y8-y13 = 0
-y7-y8+y9 = 0
-y3-y9+y10 = 0
y3-y10+y11 = 0
-y11 + y13 = 0
Исходя из исходных уравнений получаем:
y11 = y13
-y3 - y9 + y10 = y3 - y10 + y11 =>y9=y11=y13
y3 – y4 + y6 = y3 - y5 + y6 =>y4=y5
-y1 - y3 + y4 = -y2 – y3 + y4 =>y1=y2
y1 – y6 –y8 +y9 +y8=0 =>y1 = y6=y2
Следовательно, y9=y11=y13, y1=y6 =y2, y4=y5
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
y11 |
y12 |
y13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
2 |
2 |
2 |
1 |
1 |
2 |
1 |
2 |
1 |
2 |
Отсюда можно сделать вывод, что наличие положительных значений (больше 0) показывают, что p - цепь полная и является инвариантной.
Рассмотрим
матричное уравнение:
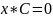 ,
,
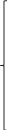 Согласно
этому уравнению, получаем:
Согласно
этому уравнению, получаем:
-x1+x5 = 0
-x1-x2+x3+x4-x7+x8 = 0
x1-x3 = 0
x2-x4 = 0
x3+x4-x5 = 0
x5 - x6 = 0
x5 - x6 = 0
x6 - x7 = 0
x7 - x8 = 0
x8 – x9 =0
Исходя из исходных уравнений получаем:
x1=x5
x1=x3 => x3 =x5
x2=x4
x5=x6 => x6=x3=x1=x5
x6=x7 => x7=x6=x3=x1=x5
x7=x8 => x8=x7=x6=x3=x1=x5
x8=x9 => x9=x8=x7=x6=x3=x1=x5
Следовательно, x9=x8=x7=x6=x3=x1=x5, x2=x4
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
Отсюда можно сделать вывод, что наличие положительных значений (больше 0) показывают, что t - цепь полная и является последовательной.
Вывод: Конечная СП-модель является ограниченной, т.к. количество маркировок не превышает допустимого значения (k = 2) и живой, что показывает последовательность цепи. Таким образом сеть является безопасной.
