МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
	Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
	«Московский технический университет связи и информатики»

Кафедра «Математическая кибернетика и информационные технологии»

Практическая работа №1

по дисциплине:

«Интеллектуальные системы»

на тему:

«Изучение способов представления и исследования сетей Петри»

Вариант №2

г. Москва 2025

Цель работы:

Изучение матричных способов представления сетей Петри (СП) и методов исследования СП-моделей на основе матричных уравнений и дерева достижимых разметок (ДДР).

Задание:

1. Выбрать структуру СП в соответствии с номером варианта;

2. Описать заданную СП-модель с помощью матриц F, H, 0;

3. Провести исследование СП-модели на основе матричных методов. Сделать заключение о живости и безопасности сети;

4. Провести исследование СП-модели путем построения дерева достижимых разметок (ДДР) вручную и с использованием программного комплекса. Сравнить полученные результаты;

5. На основе проведенных исследований оценить корректность СП-модели и предложить варианты устранения недостатков в случае их обнаружения. Допустимо добавлять новые элементы и ограниченно видоизменять топологию сети. Полученная модель должна отвечать требованиям живости и безопасности;

6. Провести исследование полученной сети с помощью матричных методов и ДДР;

7. Сравнить изученные способы анализа СП и сформулировать методику их совместного использования для исследования СП-моделей вычислительных систем;

Ход работы:

Выберем структуру сети Петри в соответствии с № варианта

Сделаем графическое описание сети Петри для позиций и переходов.

Описание обозначений:

P = {p1….p8} – множество позиций.

|P| = 8 – мощность позиций

T = {t1…..t7} – множество переходов.

|T| = 7 – Мощность переходов

Описание заданной модели с помощью матрицы F, H, μ0:

Для нахождения функции инцидентности следует использовать формулу: F: PxT;

Результат матрицы связей позиций:

F	t1	t2	t3	t4	t5	t6	t7
p1	1	0	0	0	0	0	0
p2	0	1	0	0	0	0	0
p3	0	0	1	1	0	0	0
p4	0	0	0	0	1	0	0
p5	0	0	1	0	0	1	1
p6	0	0	0	0	0	1	0
p7	0	0	0	0	1	1	0
p8	0	0	0	0	0	0	1

Для нахождения функции инцидентности следует использовать формулу: H: TxP;

Результат матрицы связей переходов:

H	p1	p2	p3	p4	p5	p6	p7	p8
t1	0	1	1	1	0	0	0	0
t2	0	0	0	0	1	0	0	0
t3	0	0	0	0	0	1	0	0
t4	0	0	0	0	0	0	1	0
t5	0	0	0	0	0	0	0	1
t6	1	0	0	0	0	0	0	0
t7	1	0	0	0	0	0	0	0

Начальная разметка сети выглядит: μ0 {1;0;0;0;0;0;0;0}

Исследование СП-модели на основе матричных методов

С помощью матричных методов можно показать, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтвержда­ется, то можно заключить, что описываемая система содержит не­которые недоработки.

Введём в рассмотрение матрицу С, которая получается следующим образом:

С = H^T – F, где H^T – транспонированная матрица H.

Пусть размерность С равна n x m, где m и n – мощности множеств P и T, тогда

H^T =

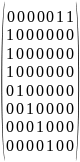
С= - =

Рассмотрим матричное уравнение: y * C = 0.

Согласно матрицы составим систему уравнений:

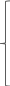-y₁+y₂+y₃+y₄ = 1

-y₂+y₅ = 0

-y₃+y₅+y₆ = 1

-y₃+y₇ =0

-y₄+y₈ = 0

y₁+y₅-y₆-y₇ = 1

y₅-y₈ = 0

Решаем систему уравнений:

y₁=y₃=y₇=1

y₂=y₄=y₅=y₇=0

y={1;0;1;0;0;1;0}

Отсюда можно сделать вывод, что p – цепь неполная, т.к. имеются 0, поэтому система не является инвариантной.

Рассмотрим матричное уравнение y * C * x = 0, составив

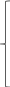систему уравнений согласно матрицы

-x1 + x6 = 0 (1) x1 - x2 = 0 (2) x1 - x3 – x4 = 0 (3) x1 - x5 =0 (4) x2 - x3 - x6 – x7 = 0 (5) x3 - x6 = 0 (6) x5 - x7 = 0 (7)

После решения уравнения получается следующее решение:

x₂=x₃=x₅=1

x₁=x₄=x₅=x₇=0

y={0;1;1;0;0;1;0}

Из полученных данных можно сделать вывод, t – цепь неполная, соответственно система не является последовательной и небезопасной.