
Волны курсовая
.docxФедеральное агентство связи
Ордена Трудового Красного Знамени
Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Московский технический университет связи и информатики»
Кафедра
Техническая электродинамика и антенны
Дисциплина
Электродинамика и распространение радиоволн
КУРСОВАЯ РАБОТА
Анализ электромагнитного поля в диэлектрическом волноводе
Вариант №11
Выполнил студент:
Группа:
Проверила:
Федотова Т. Н.
Москва 2024 г
Задание

Исходные данные

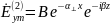


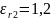

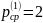

Решение
С помощью уравнений Максвелла записать выражения для всех остальных составляющих векторов
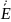 и
и
 в средах 1 и 2.
в средах 1 и 2.
Определим комплексные амплитуды всех проекций в средах 1 и 2.
Уравнение связи:
Найдем

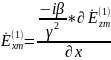

Так
как
 по условию =>
по условию =>

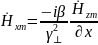

Уравнение
Максвелла, связывающее поле
 и
и
 :
:


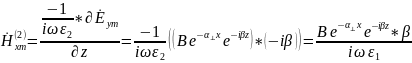


Итого:












На основе граничных условий и связи поперечных волновых чисел с коэффициентом распространения
 составить уравнения для определения
поперечных волновых чисел
составить уравнения для определения
поперечных волновых чисел
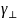 и
и
 .
Решить уравнения (например, графическим
способом относительно
и
).
.
Решить уравнения (например, графическим
способом относительно
и
).
Рассмотрим
применение граничных условий на границе
раздела (при
 ):
):
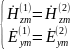

После преобразования получим:

Делим второе на первое
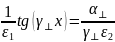
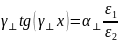
Запишем уравнение Гельмгольца для получения равенства между суммой квадратов поперечных волновых чисел.








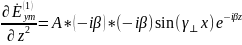

-

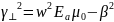


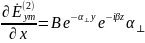



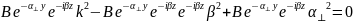
-
Имеем:
 – абсолютная
диэлектрическая проницаемость первой
среды
– абсолютная
диэлектрическая проницаемость первой
среды
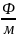
 – абсолютная
диэлектрическая проницаемость второй
среды
– абсолютная
диэлектрическая проницаемость второй
среды
 – электрическая
постоянная
– электрическая
постоянная
 – магнитная
постоянная
– магнитная
постоянная

 – циклическая
частота электромагнитных колебаний
– циклическая
частота электромагнитных колебаний
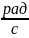
 – частота
электромагнитных колебаний
– частота
электромагнитных колебаний
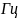
 – радиус
окружности
– радиус
окружности


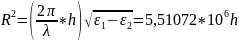





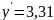
Вернёмся к замене:

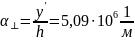
Определить обеспечивается ли одноволновый (одномодовый) режим работы световода на частоте
 .
Если условие не выполняется, определеить
максимальную толщину световода для
его выполнения.
.
Если условие не выполняется, определеить
максимальную толщину световода для
его выполнения.
Толщина
световода
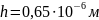 не
обеспечивает условие одномодового
режима,
т.к.
не
обеспечивает условие одномодового
режима,
т.к.
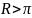 .
.
Предположим:




На новом графике:


Тогда:
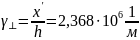
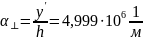
Для средней толщины световода определить параметры для волны низшего типа , и .
и уже найдены:
Для нахождения используются две данные формулы:





Фазовая скорость:

Используя заданную величину
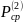 определить постоянные
определить постоянные
 и
и
 для низшего типа волны.
для низшего типа волны.

Запишем выражение для вектора Пойнтинга во 2-й среде. Комплексный вектор Пойнтинга определяется как половина векторного произведения комплексной амплитуды вектора напряжённости электрического поля на комплексно-сопряжённое комплексной амплитуды вектора напряжённости магнитного поля:

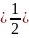
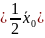
Запишем выражение для :
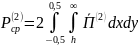






Рассчитать и построить зависимости амплитуд всех составляющих полей от координаты
 для низшего типа волны в средах 1 и 2.
для низшего типа волны в средах 1 и 2.




Вывод
Были
определены комплексные амплитуды всех
проекций векторов
 и
и
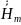 в средах 1 и 2 при
в средах 1 и 2 при
 .
.
Составлены и совестно были решены уравнения, которые связывают между собой неизвестные поперечные волновые числа в средах 1 и 2.
Определены максимальная толщина волновода, при которой по нему будет распространяться только волна низшего типа.
Вычислены параметры для волны низшего типа при средней толщине световода.
Используя заданную величину единичной мощности волны, были вычислены амплитуды и для среды 2, входящие в выражения всех проекций векторов и .
Были
построены зависимости амплитуд всех
проекций векторов
и
от координаты
в области
и в области
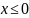 .
.
