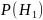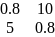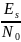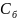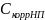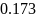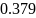Федеральное агентство связи
Ордена трудового красного знамени федеральное государственное
бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Радиотехнических систем
Практическая работа №2
«МОДЕЛИРОВАНИЕ АЛГОРИТМА ОПТИМАЛЬНОГО ОБНАРУЖЕНИЯ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ НА ФОНЕ БЕЛОГО ШУМА В СРЕДЕ СПЕКТР-2»
Вариант 8
Выполнил студент
Проверила:
Москва, 2025
Цель практикума.
Экспериментальное исследование алгоритма оптимального обнаружения детерминированных сигналов на фоне белого шума.
Домашний расчет по определению порогов обнаружителя в зависимости от априорной информации и отношения сигнал/шум (ОСШ).
Исходные данные варианта 8
Характеристический многочлен, порождающий M -последовательность |
|
|
|
|
10010001011 |
0.0022 |
2.0138 |
0.725 |
|
Расчёт абсолютного порога производится по следующим формулам:
Критерий Байеса.
По критерию Байеса абсолютный порог равен:

где π - показатель риска (потерь), π10 - потери при ложной тревоге, π 00 - при правильном принятии гипотезы H0 (принятие решения об отсутствии сигнала в принятой выборке), π10 - при пропуске цели, π 01 - при правильном принятии гипотезы H1 ( принятие решения о наличии сигнала в принятой выборке).

Критерий идеального наблюдателя При использовании критерия идеального наблюдателя порог вычисляется по следующей формуле:

где
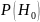 ,
,
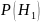 -
априорные вероятности справедливости
гипотезы
-
априорные вероятности справедливости
гипотезы
 и
и
 соответственно.
соответственно.
Критерий максимума правдоподобия По критерию максимума отношения правдоподобия абсолютный порог равен:
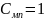
Определение порога для корреляционного обнаружителя Порог для корреляционного обнаружителя определяется по формуле:
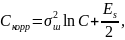
где
 - дисперсия белого гауссовского шума.
- дисперсия белого гауссовского шума.
Тогда для критерия Байеса:
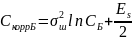
Для критерия идеального наблюдателя:
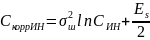
Для критерия максимума отношения правдоподобия соответственно:

Критерий Неймана-Пирсона Для сигнала с известной начальной фазой порог по критерию НейманаПирсона будет определяться как:

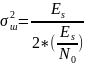

Рассчитанные пороги для ОСШ в диапазоне от 5 до 15 дБ
|
|
|
|
|
|
|
|
|
5 |
|
|
|
323.5 |
455.7 |
709.4 |
|
2317 |
6 |
|
|
|
257 |
572.4 |
773.9 |
|
2065 |
7 |
|
|
|
204 |
665.1 |
825.13 |
|
1840 |
8 |
|
|
|
162 |
738.7 |
865.8 |
|
1640 |
9 |
|
|
1 |
129 |
797.2 |
898.2 |
1023 |
1462 |
10 |
|
|
|
102.3 |
843.6 |
923.8 |
|
1303 |
11 |
|
|
|
81.3 |
880.5 |
944.2 |
|
1161 |
12 |
|
|
|
64.5 |
909.8 |
960.4 |
|
1035 |
13 |
|
|
|
51.3 |
933.1 |
973.3 |
|
922.4 |
14 |
|
|
|
40.7 |
951.6 |
983.5 |
|
822.1 |
15 |
|
|
|
32.4 |
966.3 |
991.6 |
|
732.7 |
Измерения Для критерия Байеса
|
|
Pобн |
Pпц |
Pлтр |
Pпротс |
|
455.7 |
323.5 |
0.972 |
0.0254 |
0.285 |
0.711 |
3.16 |
572.4 |
257 |
0.978 |
0.022 |
0.216 |
0.785 |
3.98 |
665.1 |
204 |
0.985 |
0.016 |
0.149 |
0.851 |
5.01 |
738.7 |
162 |
0.988 |
0.012 |
0.098 |
0.901 |
6.31 |
797.2 |
129 |
0.991 |
0.0085 |
0.059 |
0.94 |
7.926 |
843.6 |
102.3 |
0.996 |
0.003 |
0.033 |
0.967 |
9.989 |
880.5 |
81.3 |
0.997 |
0.002 |
0.0154 |
0.984 |
12.575 |
909.8 |
64.5 |
0.999 |
0.0006 |
0.005 |
0.994 |
15.85 |
933.1 |
51.3 |
0.9996 |
0.00034 |
0.0023 |
0.9978 |
19.93 |
951.6 |
40.7 |
0.9999 |
0.00007 |
0.0006 |
0.9995 |
25.1 |
966.3 |
32.4 |
1 |
0 |
0 |
1 |
31.5 |

По критерию идеального наблюдателя
|
σ2 |
Es/No измер |
Pобн |
Pпц |
Pлтр |
Pпротс |
709.4 |
323.5 |
3.16 |
0.95 |
0.05 |
0.191 |
0.809 |
773.9 |
257 |
3.979 |
0.961 |
0.0385 |
0.157 |
0.852 |
825.13 |
204 |
5.011 |
0.969 |
0.029 |
0.098 |
0.901 |
865.8 |
162 |
6.312 |
0.979 |
0.0203 |
0.066 |
0.933 |
898.2 |
129 |
7.926 |
0.988 |
0.012 |
0.039 |
0.9601 |
923.8 |
102.3 |
9.992 |
0.994 |
0.0071 |
0.022 |
0.97 |
944.2 |
81.3 |
12.57 |
0.997 |
0.003 |
0.01 |
0.989 |
960.4 |
64.5 |
15.83 |
0.9985 |
0.0015 |
0.004 |
0.996 |
973.3 |
51.3 |
19.9 |
0.9997 |
0.00033 |
0.0015 |
0.9987 |
983.5 |
40.7 |
25.1 |
0.9999 |
0.00011 |
0.00017 |
0.9997 |
991.6 |
32.4 |
31.5 |
0.99988 |
0.000023 |
0 |
1 |

По критерию максимума правдоподобия
CкоррМП |
σ2 |
Es/No измер |
Pобн |
Pпц |
Pлтр |
Pпротс |
1023 |
323.5 |
3.152 |
0.889 |
0.11 |
0.106 |
0.893 |
1023 |
257 |
3.97 |
0.919 |
0.081 |
0.086 |
0.914 |
1023 |
204 |
5.009 |
0.949 |
0.051 |
0.057 |
0.943 |
1023 |
162 |
6.314 |
0.9593 |
0.0407 |
0.039 |
0.961 |
1023 |
128.7 |
7.938 |
0.976 |
0.024 |
0.023 |
0.977 |
1023 |
102 |
10.013 |
0.992 |
0.0077 |
0.011 |
0.9885 |
1023 |
81 |
12.62952 |
0.998 |
0.0024 |
0.0069 |
0.993 |
1023 |
64.5 |
15.848 |
0.997 |
0.0032 |
0.002 |
0.998 |
1023 |
51 |
20.046 |
0.999665 |
0.000335 |
0.000443 |
0.999557 |
1023 |
40.7 |
25.118 |
0.999878 |
0.000122 |
0.0003 |
0.99967 |
1023 |
32.35 |
31.6237 |
1 |
0 |
0 |
1 |