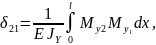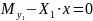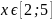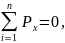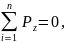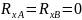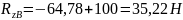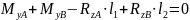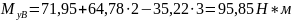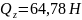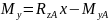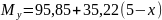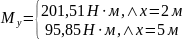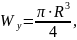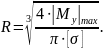идэзэшки / ПриклМех ИДЗ2.2
.docxМИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ПМИГ |
||||||
отчЁт по индивидуальному домашнему заданию №2.2 по дисциплине «Прикладная механика» Тема: Решение статически неопределенной задачи графическим методом (правило Верещагина)
|
||||||
|
||||||
Санкт-Петербург 2025 |
содержание
|
ИСХОДНЫЕ ДАННЫЕ |
3 |
|
РАСЧЕТНАЯ ЧАСТЬ |
5 |
2.1. |
Выбор декартовой системы координат |
5 |
2.2 |
Определение грузовых участков |
5 |
2.3. |
Раскрытие статической неопределенности графическим методом |
5 |
2.4. |
Нахождение
|
6 |
2.5. |
Расчет реакции в заделке |
14 |
2.6. |
Расчёт изгибающего момента My и поперечной силы Qz на каждом грузовом участке методом сечений |
15 |
2.7. |
Построение эпюр My и Qz |
17 |
2.8. |
Определение диаметра стержня |
17 |
|
ПРИЛОЖЕНИЕ А |
18 |
|
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ |
20 |
ИСХОДНЫЕ ДАННЫЕ
Для расчётов были использованы данные, которые представлены в таблице 1 и на рисунке 1. На том же рисунке изобразили необходимые по заданию эпюры.
|
Рисунок 1 – Расчётная схема для задания с эпюрами |
Таблица 1 – Геометрические параметры и внешние силы
Длина участка, м |
Сосредоточенная сила Р, Н |
Материал |
|
l1 |
l2 |
P |
Медь М1 |
2 |
3 |
100 |
|
Требуется:
1) Раскрыть статическую неопределенность графическим методом
2) Построить эпюры Qx и My
3) Из условия прочности стержня определить диаметр стержня
РАСЧЁТНАЯ ЧАСТЬ
Выбор декартовой системы координат
Система координат нанесена на рисунке 1.
Определение грузовых участков
Грузовые участки обозначены на рисунке 1.
Раскрытие статической неопределенности графическим методом
Метод
сил заключается в мысленном отбрасывании
заделки. Искомые реакции ( заменяем силами
заменяем силами
 соответственно.
соответственно.

Рисунок 2 – Схема с отброшенной левой заделкой
Рассмотрим
перемещение стержня от
 .
.
Сумма этих перемещений должная равняться 0, т.к. слева (рисунок 2) есть заделка, которая не дает перемещаться стержню:

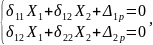
где
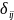 – перемещение стержня от единичной
силы
– перемещение стержня от единичной
силы
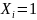 .
.
Перемещения вычисляются с помощью интегралов Морра:
|
(1) |
|
(2) |
|
(3) |
|
(4) |
|
(5) |
|
(6) |
2.4 Найдем методом сечения:
Найдем
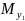 :
:

Рисунок 3 – Схема для нахождения
Откидываем заделку по методу сечений:

Рисунок 4 – Схема для нахождения методом сечения
|
|
|
|
Момент My1 определили из условия равновесия системы, которое записывается в виде уравнения (7).
|
(7) |
|
|
|
|
Рассчитаем
перемещение
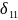 графическим методом:
графическим методом:
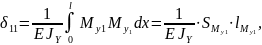
где
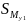 -
площадь эпюры
-
площадь эпюры
 ,
,
 – высота эпюры
.
– высота эпюры
.

Рисунок 5 - Схема для нахождения
Найдем площадь и высоту эпюры :
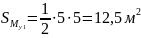

Найдем :
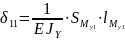

Найдем
 :
:

Рисунок 6 - Схема для нахождения
Откидываем заделку по методу сечений:

Рисунок 7 - Схема для нахождения методом сечения
|
|
|
|
Момент My2 определили из условия равновесия системы, которое записывается в виде уравнения (7).
|
(7) |
|
|
|
|
Рассчитаем
перемещение
 графическим методом:
графическим методом:


Рисунок 8 - Схема для нахождения
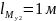
Найдем :
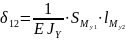

Рассчитаем
перемещение
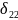 графическим методом:
графическим методом:


Рисунок 9 - Схема для нахождения
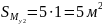
Найдем :
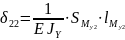

Найдем
 :
:

Рисунок 10 - Схема для нахождения
Откидываем заделку по методу сечений:

Рисунок 11 - Схема для нахождения методом сечения
|
|
|
|
Момент Myp определили из условия равновесия системы, которое записывается в виде уравнения (7).
|
(7) |
|
|
|
|
Рассчитаем
перемещение
 графическим методом:
графическим методом:


Рисунок 12 - Схема для нахождения

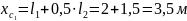


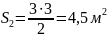
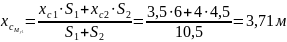


Рассчитаем
перемещение
 графическим методом:
графическим методом:
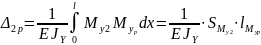

Рисунок 13 - Схема для нахождения
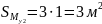

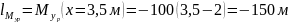

Составим систему уравнений перемещений:

Умножим второе уравнение на 2,5:

Отнимем второе уравнение из первого:


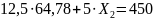
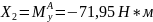
2.5 Расчет реакции в заделке
Реакцию в опорах рассчитали из условий статического равновесия системы (8) – (10).
|
(8) |
|
(9) |
|
(10) |
где Px – проекция силы на ось х,
Pz – проекция силы на ось z,
M0y – значение момента по оси y относительно полюса 0.
Из уравнения (1):
|
|
Из уравнения (2):
|
|
|
|
Из уравнения (3):
|
|
|
|
|
|
2.6 Расчёт изгибающего момента My и поперечной силы Qz на каждом грузовом участке методом сечений
Рассмотрим первый грузовой участок:

Рисунок 14 – Расчётная схема 1-го грузового участка
|
|
|
|
Поперечную силу Qz определили из условия равновесия системы, которое записывается в виде уравнения (8).
|
|
|
|
|
|
Изгибающий момент My определили из условия равновесия системы, которое записывается в виде уравнения (9).
|
|
|
|
|
|
|
|
Отдельно рассмотрели граничные условия.
|
|
Рассмотрим второй грузовой участок:

Рисунок 15 – Расчётная схема 2-го грузового участка
|
|
|
|
Поперечную силу Qz определили из условия равновесия системы, которое записывается в виде уравнения (8).
|
|
|
|
|
|
Изгибающий момент My определили из условия равновесия системы, которое записывается в виде уравнения (9).
|
|
|
|
|
|
|
|
Отдельно рассмотрели граничные условия.
|
|
2.7 Построение эпюр My и Qz
Необходимые эпюры изображены на рисунке 1.
2.8 Определение диаметра стержня
Опасным
является сечение
 ,
где изгибающий момент принимает
максимальное значение. В нашем случае
,
где изгибающий момент принимает
максимальное значение. В нашем случае
 при
x
= 2 м.
при
x
= 2 м.
Определили
наибольшие нормальные напряжения
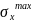 в опасном сечении по формуле (11):
в опасном сечении по формуле (11):
|
(11) |
где
 –
момент
сопротивления сечения при кручении,
который находился по соотношению (12).
–
момент
сопротивления сечения при кручении,
который находился по соотношению (12).
|
(12) |
где R
– радиус
стержня.
R
– радиус
стержня.
Условие прочности стержня подчиняется выражению (13).
|
(13) |
где
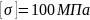 – предельно допустимое нормальное
напряжение для исследуемого материала
(меди М1[1]).
– предельно допустимое нормальное
напряжение для исследуемого материала
(меди М1[1]).
Объединяя формулы (11)-(13), получаем формулу для радиуса цилиндрического профиля (14).
|
(14) |
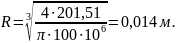
ПРИЛОЖЕНИЕ А
ИСХОДНАЯ РАСЧЕТНАЯ СХЕМА
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Воробьёв С.В., Кормилицын О.П. Анализ прочности и жёсткости стержней: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2016.

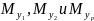 методом
сечения
методом
сечения