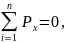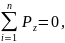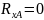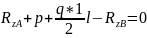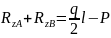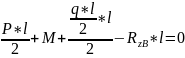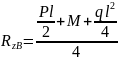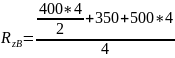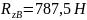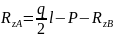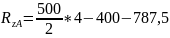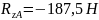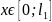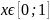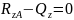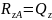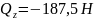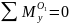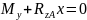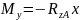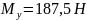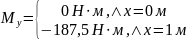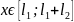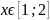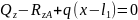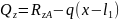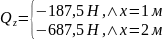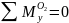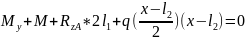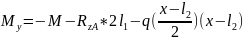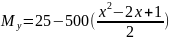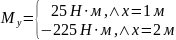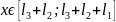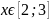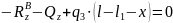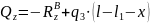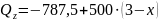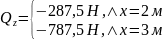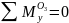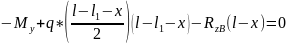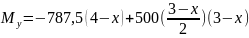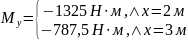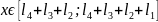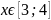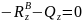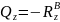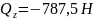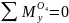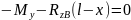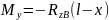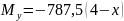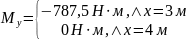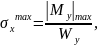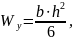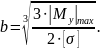идэзэшки / ПриклМех ИДЗ1.3

МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ПМИГ

отчЁт по индивидуальному домашнему заданию №1 по дисциплине «Прикладная механика» Тема: Расчёт параметров напряженного деформированного состояния в процессах растяжения-сжатия, кручения и плоско-поперечного изгиба стержня

Студент гр. ____________________ Преподаватель __________________________ Титов А.В.

Санкт-Петербург 2025

содержание

	ИСХОДНЫЕ ДАННЫЕ	3
	РАСЧЕТНАЯ ЧАСТЬ	5
2.1.	Выбор декартовой системы координат	5
2.2	Определение грузовых участков	5
2.3.	Расчет реакций в опоре	5
2.4.	Расчёт изгибающего момента My и поперечной силы Qz на каждом грузовом участке методом сечений	6
2.5.	Построение эпюр My и Qz	10
2.6.	Определение положения опасного сечения	10
2.7.	Подбор размеров прямоугольного поперечного сечения	11
	ПРИЛОЖЕНИЕ А	12
	СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ	13

1. ИСХОДНЫЕ ДАННЫЕ

Для расчётов были использованы данные, которые представлены в таблице 1 и на рисунке 1. На том же рисунке изобразили необходимые по заданию эпюры.

Рисунок 1 – Расчётная схема для задания с эпюрами

Таблица 1 – Геометрические параметры и внешние силы

Длина участка, м				Сосредоточенная сила Р, Н		Сосредоточенный момент М, Н*м		Распределённая сила q, Н/м
l1	l2	l3	l4		P		М		q
1	1	1	1		400		350		500

Требуется:

1) Построить эпюры внутренних сил Q_x и M_y

2) Определить положение опасного сечения

3) Из условия прочности стержня определить размеры стержня

2. РАСЧЁТНАЯ ЧАСТЬ

   1. Выбор декартовой системы координат

Система координат нанесена на рисунке 1.

2. Определение грузовых участков

Грузовые участки обозначены на рисунке 1.

3. Расчёт реакций в заделке

Реакцию в опорах рассчитали из условий статического равновесия системы (1) – (3).

	(1)
	(2)
	(3)

где P_x – проекция силы на ось х,

P_z – проекция силы на ось z,

M⁰_y – значение момента по оси y относительно полюса 0.

Из уравнения (1):

Из уравнения (2):

Из уравнения (3):

Подставим RzB в уравнение (2):

4. Расчёт изгибающего момента M_y и поперечной силы Q_z на каждом грузовом участке методом сечений

Рассмотрим первый грузовой участок:

Рисунок 2 – Расчётная схема 1-го грузового участка

Поперечную силу Q_z определили из условия равновесия системы, которое записывается в виде уравнения (2).

Изгибающий момент M_y определили из условия равновесия системы, которое записывается в виде уравнения (3).

Отдельно рассмотрели граничные условия.

Рассмотрим второй грузовой участок:

Рисунок 3 – Расчётная схема 2-го грузового участка

Поперечную силу Q_z определили из условия равновесия системы, которое записывается в виде уравнения (2).

Отдельно рассмотрели граничные условия.

Изгибающий момент M_y определили из условия равновесия системы, которое записывается в виде уравнения (3).

Отдельно рассмотрели граничные условия.

Рассмотрим третий грузовой участок:

Рисунок 4 – Расчётная схема 3-го грузового участка

Поперечную силу Q_z определили из условия равновесия системы, которое записывается в виде уравнения (2).

Отдельно рассмотрели граничные условия.

Изгибающий момент M_y определили из условия равновесия системы, которое записывается в виде уравнения (3).

Отдельно рассмотрели граничные условия.

Рассмотрим четвертый грузовой участок:

Рисунок 5 – Расчётная схема 4-го грузового участка

Поперечную силу Q_z определили из условия равновесия системы, которое записывается в виде уравнения (2).

Изгибающий момент M_y определили из условия равновесия системы, которое записывается в виде уравнения (3).

Отдельно рассмотрели граничные условия.

5. Построение эпюр M_y и Q_z

Необходимые эпюры изображены на рисунке 1.

6. Определение положения опасного сечения

Опасным является сечение 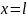, где изгибающий момент принимает максимальное значение. В нашем случае 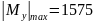при x = 3 м.

Определили наибольшие нормальные напряжения в опасном сечении по формуле (4):

(4)

где 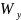– момент сопротивления сечения при кручении, который находился по соотношению (5).

(5)

где 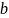и 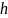– ширина и высота прямоугольного профиля, между которыми выполняется соотношение .

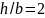7. Подбор размеров прямоугольного поперечного сечения

Условие прочности стержня подчиняется выражению (6).

(6)

где 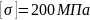– предельно допустимое нормальное напряжение для исследуемого материала ковара НМ 29^[1].

Объединяя формулы (4)-(6), получаем формулу для ширины прямоугольного профиля (7).

(7)

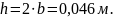
ПРИЛОЖЕНИЕ А

ИСХОДНАЯ РАСЧЕТНАЯ СХЕМА

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Воробьёв С.В., Кормилицын О.П. Анализ прочности и жёсткости стержней: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2016.