Метод двух узлов
Метод
двух узлов является частным случаем
метода узловых потенциалов и наиболее
рационален для расчёта цепей, содержащих
два узла. Для расчёта методом двух узлов
находят напряжение между этими двумя
узлами
.
Нужно определить напряжение между двух
узлов и исходя из этого вычислить все
токи в ветвях. Схема представлена на
рисунке 6.
Рисунок 6 – схема ЭЦ для метода двух узлов
Так
как данный метод является частным
случаем рассмотренного выше метода, то
потенциалы узлов уже определены и равны:
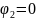и
=
13.96 В. Поэтому падение напряжения между
узлами 1 и 2 будет равно разности их
потенциалов. Ток в данном случае находится
идентичным образом, что и в предыдущем
пункте. Для расчетов по методу двух
узлов, стоит смотреть в предыдущий
пункт.
Метод наложения
Произвольно выбранное направление всех токов на исходной схеме представлено на рисунке 7.
Рисунок 7 – Произвольно выбранное направление токов на исходной схеме
Положить
равными нулю все источники ЭДС и тока
кроме первого. При этом независимые
источники, ЭДС которых равна нулю,
заменяется короткозамкнутыми отрезками.
Так как в схеме присутствует источник
тока, то при удалении его из схемы
остается разрыв цепи. Соответственно,
ветвь, содержащая ранее источник тока,
в расчёте токов при
не участвует. Для удобства частичные
токи обозначаются штрихами. Схема для
расчета методом наложения представлена
на рисунке 8.
Рисунок 8 – схема 1 для расчета методом наложения
Так
как на представленной схеме 1 контур,
то ток
будет равен току
и вычисляться через уравнение,
представленное в выражении 22.
При
вычислении величин токов
получились
следующие значения:
А
А
Пусть источник ЭДС отключён. Метод вычисления частичных токов остаётся прежним, что продемонстрировано на рисунке 9.
Рисунок 9 – Схема 2 для расчета методом наложения
Так
как на схеме присутствует источник
тока, то ток
.
Для
определения тока
необходимо
решить уравнение, представленное в
выражении 23.
Для
определения тока
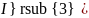необходимо
решить уравнение, представленное в
выражении 24.
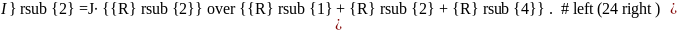
При
вычислении величин токов
получились
следующие значения:
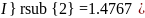
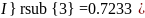
Чтобы вычислить общий ток, необходимо просуммировать частичные. Если частичный ток, направлен в противоположную сторону, нежели предполагаемый истинный ток, изображённый на рисунке 7, то значение частичного тока, берётся отрицательным.
Формула
для вычисления тока
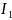представлена в выражении 25.
Формула для вычисления тока представлена в выражении 26.
Ток
равен величине тока
.
При вычислении величин токов
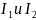получились следующие значения:
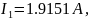
Ответ:
Расчёт тока в сопротивлении r1 методом эквивалентного генератора эдс
С
помощью метода эквивалентного источника
ЭДС определить ток в сопротивлении
.
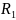Произвольно выбираем направление
искомого тока I в ветви на исходной схеме
(рисунок 10)
Рисунок 10 – Произвольно выбранное направление тока через сопротивление
Схема с исключенной ветвью из исходной схемы для вычисления относительно узлов 1 и 2 методом эквивалентного источника ЭДС напряжение холостого хода Uхх изображена на рисунке 11.
Рисунок 11 – Схема для нахождения напряжения холостого хода. Эквивалентный генератор
Для определения сопротивления генератора необходимо на месте всех ветвей с источником тока разорвать цепь, закоротить все источники ЭДС и определить сопротивление генератора.
Как
видно из схемы на рисунке 12, сопротивление
генератора
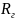равно сопротивлению
.
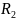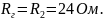
Рисунок 12 – Схема сопротивления эквивалентного генератора.
Теперь
необходимо определить ЭДС генератора
(
).
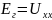Для этого необходимо пройти любым путём
от узла 1 до узла 2, при этом обязательно
обходя пути с источником тока. Обозначить
падения напряжения на встречающихся
элементах, рассчитать их и сложить.
Путь выбранный для расчёта ЭДС генератора представлен на рисунке 13.
Рисунок 13 – Путь расчёта ЭДС генератора
Так как через ЭДС и сопротивления протекает ток источника, то согласно этому, формула для вычисления напряжения холостого хода между узлами 1 и 2 представлена в выражении 27.
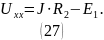
Подставив
числовые значения, получается, что
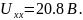
Для нахождения тока в ветви, содержащей сопротивление необходимо составить и решить уравнение, представленное в выражении 28.
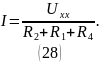
Подставив числовые значения в выражение
28, находится величина тока
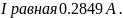
Ответ:
